Một chất điểm chuyển động thẳng đều trên trục Ox với phương trình x=100-10t (m,s). a) Vẽ đồ thị tọa độ thời gian của chất điểm b) Trên đồ thị hãy vẽ điểm M biểu diễn vị trí của chất điểm tại thời điểm t-5s
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
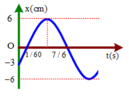
Vật chuyển động về phía âm của trục tọa độ nên v = -4 m/s.
Ban đầu (t = 0) thì x0 = 20.
Vậy phương trình chuyển động của chất điểm là x = 20 – 4t (m)

Chọn: A.
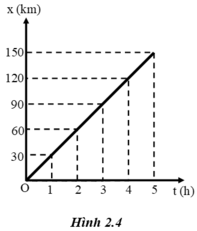
Theo đồ thị, khi t = 0 thì x0 = 0.
Sau mỗi giây ôtô đi được quãng đường 30km nên v = 3 km/h
=> phương trình chuyển động của ô tô là: x = 30t (km; h).

Chọn: A.
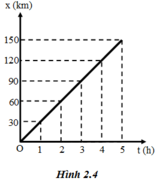
Theo đồ thị, khi t = 0 thì x0 = 0.
Sau mỗi giây ôtô đi được quãng đường 30km nên v = 3 km/h
=> phương trình chuyển động của ô tô là: x = 30t (km; h).

Chọn: D
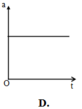
Trong chuyển động thẳng đều, vận tốc không thay đổi theo thời gian nên đồ thị biểu diễn vận tốc theo thời gian trong hệ tọa độ vuông góc Otv có dạng là một đường thẳng song song với trục thời gian Ot.

Chọn: D.
Trong chuyển động thẳng đều, vận tốc không thay đổi theo thời gian nên đồ thị biểu diễn vận tốc theo thời gian trong hệ tọa độ vuông góc Otv có dạng là một đường thẳng song song với trục thời gian Ot.

\(b,\text{PT giao Ox và Oy: }\\ y=0\Leftrightarrow x=\dfrac{3}{2}\Leftrightarrow A\left(\dfrac{3}{2};0\right)\Leftrightarrow OA=\dfrac{3}{2}\\ x=0\Leftrightarrow y=3\Leftrightarrow B\left(0;3\right)\Leftrightarrow OB=3\\ \Leftrightarrow S_{OAB}=\dfrac{1}{2}OA\cdot OB=\dfrac{1}{2}\cdot\dfrac{3}{2}\cdot3=\dfrac{9}{4}\left(cm^2\right)\\ c,C_1:\text{Áp dụng Pytago: }AB=\sqrt{OA^2+OB^2}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\\ C_2:AB=\sqrt{\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2}=\sqrt{\left(\dfrac{3}{2}-0\right)^2+\left(0-3\right)^2}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\)

Chọn B.
Chuyển động thẳng đều là chuyển động có vận tốc không thay đổi theo thời gian.
Đồ thị B cho thấy đường biểu diễn v theo thời gian là một đường nằm ngang nên v không đổi theo t và biểu diễn một chuyển động thẳng đều.