a) tính góc ABC

a: Xét ΔBAD và ΔBHD có 

BA=BH

\(\widehat{ABD}=\widehat{HBD}\)

BD chung

Do đó: ΔBAD=ΔBHD

CM : a) Xét tam giác ABD và tam giác HBD

có AB = BD (gt)

   góc DBA = góc HBD (gt)

  BD : chung

=> tam giác ABD = tam giác HBD (c.g.c) (Đpcm)

b) Ta có : tam giác ABD = tam giác HBD (cm câu a)

=> góc A = góc DHB ( hai góc tương ứng)

Mà góc A =90⁰ => góc DHB = 90⁰ 

                      => DH vuông góc với BC

c) Xét tam giác ABC có góc A = 90⁰

=> góc B + góc C = 90⁰ (t/c của 1 tam giác)

=> góc B = 90⁰ - góc C = 90⁰ - 36⁰ = 54⁰

Ta có : góc HBD = góc DBA = góc B/2 = 54⁰/2 = 27⁰

Xét tam giác ADE có A = 90⁰

=> góc ADB + góc DBA = 90⁰ (t/c của 1tam giác)

=> góc ADE = 90⁰ - góc ADB = 90⁰ - 27⁰ = 63⁰

(Em tự vẽ hình, ghi GT-KL nhé)

a) Xét \(\Delta ABD\)và \(\Delta HBD\)có:

AB = BH (gt)

^ABD = ^HBD (gt)

BD chung

=> \(\Delta ABD=\Delta HBD\left(c.g.c\right)\)

b) Ta có: \(\Delta ABD=\Delta HBD\left(cmt\right)\)

=> ^BAD = ^BHD = 90^o 

=> \(DH\perp BC\)

c) 

\(\Delta ABC\)có : ^BAC + ^ABC + ^CBA = 180^o

=> ^ABC = 180^o- 90^o- 36^o = 54^o

=> ^DBC = 1/2 ^ABC = 37^o

\(\Delta BDC\): ^ADB là góc ngoài tại đỉnh D

=> ^ADB = ^DBC + ^DCB = 37^o + 36^o = 73^o

Chúc em học tốt!!!

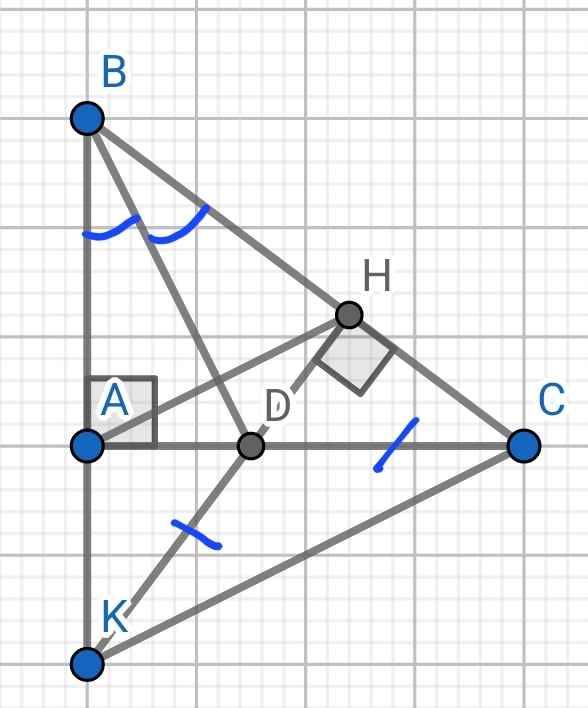
a) Xét hai tam giác vuông: ∆ABD và ∆HBD có:

BD chung

∠ABD = ∠HBD (BD là phân giác của ∠ABH)

⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)

b) Do ∆ABD = ∆HBD (cmt)

⇒ AB = BH (hai cạnh tương ứng)

⇒ B nằm trên đường trung trực của AH (1)

Do ∆ABD = ∆HBD (cmt)

⇒ AD = HD (hai cạnh tương ứng)

⇒ D nằm trên đường trung trực của AH (2)

Từ (1) và (2) ⇒ BD là đường trung trực của AH

c) Xét ∆ADK và ∆HDC có:

AD = HD (cmt)

∠ADK = ∠HDC (đối đỉnh)

DK = DC (gt)

⇒ ∆ADK = ∆HDC (c-g-c)

⇒ ∠DAK = ∠DHC (hai góc tương ứng)

⇒ ∠DAK = 90⁰

Mà ∠DAB = 90⁰

⇒ ∠DAK + ∠DAB = 180⁰

⇒ B, A, K thẳng hàng

Mọi người giúp Em với 

a) Xét \(\Delta ABD\)và \(\Delta HBD\)có:

\(BA=BH\left(gt\right)\)

\(\widehat{ABD}=\widehat{HBD}\)(ad là tia phân giác của \(\widehat{B}\))

\(BD\)là cạnh chung

Do đó: \(\Delta ABD=\Delta HBD\left(c.g.c\right)\)

4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha

*In đậm: quan trọng.

#)Góp ý :

Giải thì vẫn giải đc, chỉ tại dài quá, người nhìn thấy dài thì chẳng ai muốn giải đâu, vì lười, mak mún kiếm P nhanh mà, là mình thì vẫn giải đc nhưng sẽ mất tg đó, chắc 15-30p :v

a: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=3^2+4^2=25\)

=>\(BC=\sqrt{25}=5\left(cm\right)\)

b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có

BD chung

\(\widehat{ABD}=\widehat{HBD}\)

Do đó: ΔABD=ΔHBD

c: Ta có: ΔBAD=ΔBHD

=>BA=BH

Xét ΔBHI vuông tại H và ΔBAC vuông tại A có

BH=BA

góc HBI chung

Do đó: ΔBHI=ΔBAC

=>BI=BC

=>ΔBIC cân tại B

Xét ΔBIC cân tại B có \(\widehat{IBC}=60^0\)

nên ΔBIC đều

d: Ta có: DA=DH(ΔBAD=ΔBHD)

DH<DC(ΔDHC vuông tại H)

Do đó: DA<DC

Xét tam giác ABD và tam giác HBD có:

BD: chung.

Góc BAD=BHD=90 độ.

Góc ABD=HBD(Phân giác BD)

=> Tam giác ABD=tam giác HBD(ch-gn)

b/ Gọi giao điểm của BD và AH là O.

Xét tam giác AOB và tam giác HOB có:

BO:chung.

Góc ABO=HBO(Phân giác BD)

BA-BH(cạnh tương ứng của tam giác BAD=BHD)

=>Tam giác AOB=tam giác HOB(c-g-c)

=> Góc AOB=HOB(góc tương ứng)=90 độ

Góc BAH=BKC(góc ứng với cạnh đáy của tam giác cân có cùng góc B)

=> AH//KC

Mà BD vuông góc với AH nên BD cũng vuông góc với KC.

c/Xét tam giác ADK và tam giác HDC có:

DA=DH(cạnh tương ứng của tam giác BAD=tam giác BHD)

Góc DAK=DHC=90 độ.

Góc ADK=HDC(đối đỉnh)

=> tam giác ADK=tam giác HDC(g-c-g)

=> DK=DC(cạnh tương ứng)

Mà trong tam giác vuông HDC có:

DC là cạnh huyền nên DC>DH

=> DK>DH(đpcm)