Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
2: Ta có: \(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\)
\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
1: Ta có: \(A=\left(\dfrac{x-5\sqrt{x}}{x-25}-1\right):\left(\dfrac{25-x}{x+2\sqrt{x}-15}-\dfrac{\sqrt{x}+3}{\sqrt{x}+5}-\dfrac{\sqrt{x}-5}{\sqrt{x}-3}\right)\)
\(=\left(\dfrac{x-5\sqrt{x}-x+25}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\right):\dfrac{25-x-x+9-x+25}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{-5}{\sqrt{x}+5}\cdot\dfrac{\left(\sqrt{x}+5\right)\left(\sqrt{x}-3\right)}{-3x+59}\)
\(=\dfrac{-5\left(\sqrt{x}-3\right)}{-3x+59}\)
\(=\dfrac{5\sqrt{x}-15}{3x-59}\)
2: Ta có: \(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\)
\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
\(a,VT=\left[\dfrac{2}{3x}-\dfrac{2}{x+1}\cdot\dfrac{x+1-3x^2-3x}{3x}\right]\cdot\dfrac{x}{x-1}\\ =\left(\dfrac{2}{3x}-\dfrac{2}{x+1}\cdot\dfrac{\left(x+1\right)\left(1-3x\right)}{3x}\right)\cdot\dfrac{x}{x-1}\\ =\left(\dfrac{2}{3x}-\dfrac{2-6x}{3x}\right)\cdot\dfrac{x}{x-1}=\dfrac{6x}{3x}\cdot\dfrac{x}{x-1}=\dfrac{2}{x-1}=VP\left(x\ne0;x\ne1\right)\)
\(b,VT=\dfrac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\sqrt{a}}=VP\left(a\ge0;a\ne1\right)\)
nãy đăng ảnh nhưng không hiện, lại phải mất công đánh lại :Đ
a: Ta có: \(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\dfrac{x+2+\sqrt{x}\left(\sqrt{x}-1\right)-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x-\sqrt{x}-\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)
b: Ta có: \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right)\cdot\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{2}{x-1}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
1: Ta có: \(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}}{2}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}-2}{\sqrt{x}\left(x+\sqrt{x}+1\right)}\)
1: Ta có: \(P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)
\(=x-\sqrt{x}-2\sqrt{x}-1+2\sqrt{x}+2\)
\(=x-\sqrt{x}+1\)
2: Ta có: \(A=\left(\dfrac{x+2\sqrt{x}}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\left(1-\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\right)\)
\(=\dfrac{x+2\sqrt{x}-x+\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\dfrac{x+\sqrt{x}+1-\sqrt{x}-2}{\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{x+\sqrt{x}+1}{x-1}\)
\(=\dfrac{1}{x-1}\)
3: Ta có: \(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\)
\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
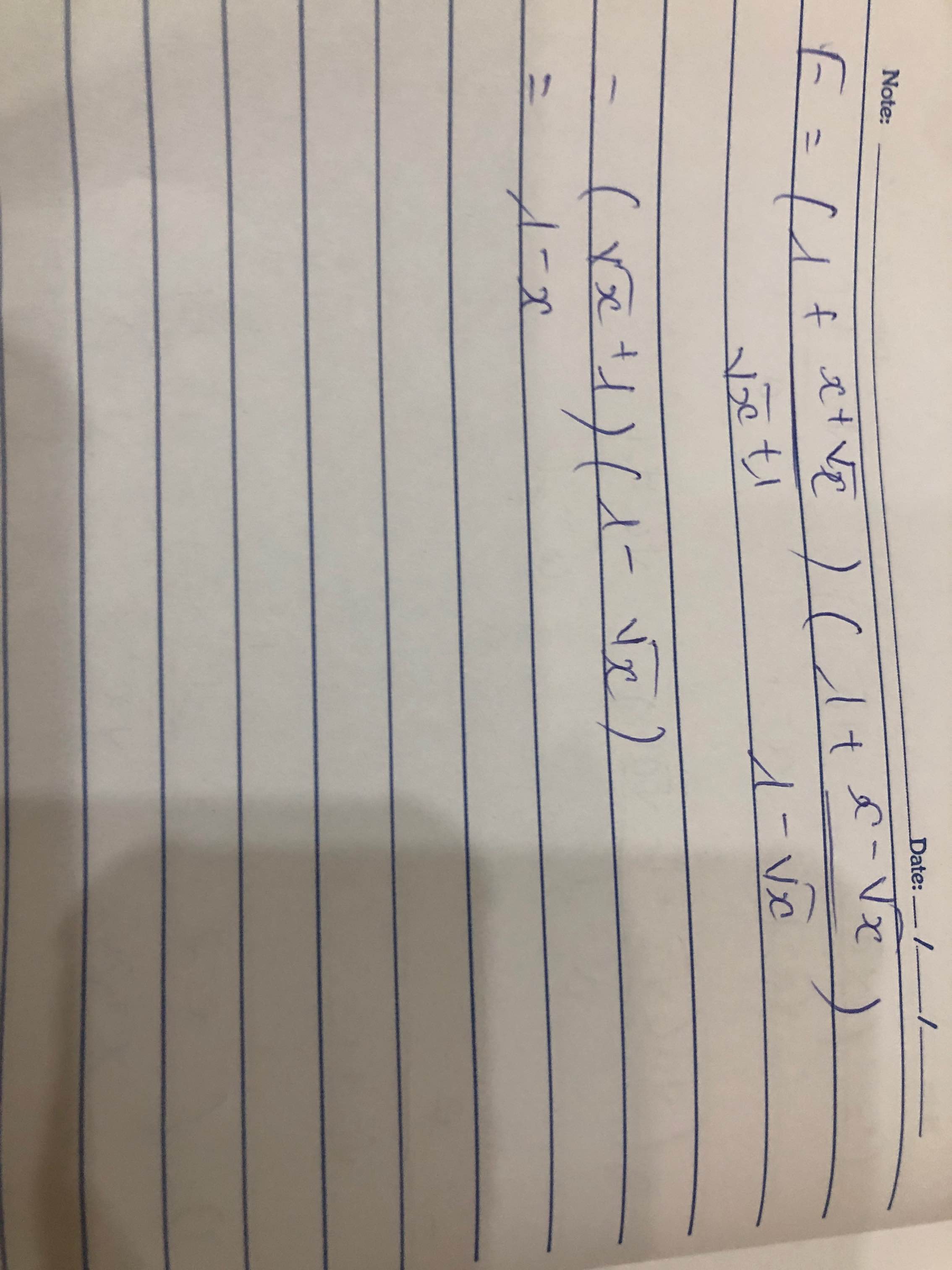
\(=\left(\dfrac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\sqrt{a}-1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\left(\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-2\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}\right)\)
=\(\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\left(\dfrac{a-1}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}-\dfrac{a-\sqrt{a}-2}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\right)\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}.\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{a-1-a+\sqrt{a}+2}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}.\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{\sqrt{a}+1}\)
\(=\dfrac{\sqrt{a}-2}{\sqrt{a}\left(\sqrt{a}+1\right)}=\dfrac{\sqrt{a}-2}{a+\sqrt{a}}\)
2, \(\left(\dfrac{1}{1-\sqrt{x}}-\dfrac{1}{1+\sqrt{x}}\right).\left(\dfrac{1}{\sqrt{x}}+1\right)\)
\(=\left(\dfrac{1+\sqrt{x}}{\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)}-\dfrac{1-\sqrt{x}}{\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)}\right)\left(\dfrac{1+\sqrt{x}}{\sqrt{x}}\right)\)
\(=\dfrac{1+\sqrt{x}-1+\sqrt{x}}{\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)}.\dfrac{1+\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)}.\dfrac{1+\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{2}{1-\sqrt{x}}\)