1. cho tam giác ABC vuông tại A có đường cao AH.Gọi M,N lần lượt là các điểm đối xứng của H qua AB và AC.CMR: đường thẳng mà là tiếp xúc với đường tròn đường kính BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 12 2015
Phần a dễ tự làm nhé.
b, Gọi MH giao AB = K
NH giao AC = T
O là trung điểm BC
=> tam giác OAB cân tại O=> góc OBA = góc OAB
phần a=>góc OBA = góc ABM
=> góc MAB + góc BAO = góc MAB + góc MBA = 90 độ
TT OAN = 90 độ
=> A , M ,N thẳng hàng
MAO = 90 độ => MA vuông góc OA => MN là tiếp tuyến của (O,OB)
CM
10 tháng 8 2017
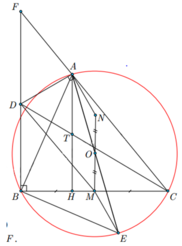
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .