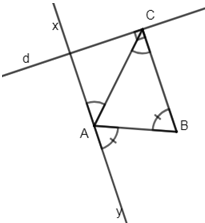
Cho tam giác ABC cân đỉnh A (\(\widehat{A}< 60^o\)), trên nửa mặt phẳng bờ AC có chứa B vẽ tia Ax sao cho \(\widehat{xAC}< \widehat{ACB}\), lấy điểm C' sao cho Ax là trung trực của CC'. Nối BC' cắt tia Ax ở D.
a) Chứng minh rằng tam giác C'DA cân
b) Tìm trên Ax điểm M sao cho chu vi tam giác MBC đạt giá trị nhỏ nhất. Chứng minh rằng khi Ax quay quanh điểm A thì độ lớn \(\widehat{BMC}\)không đổi.
c) Lấy bất kì điểm E trên cạnh AB và điểm F trên cạnh AC. Hãy so sánh độ dài AE + EF + FC với BC