Giúp em bài 16 với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a: Xét tứ giác AMCD có
I là trung điểm chung của AC và MD
góc AMC=90 độ
=>AMCD là hình chữ nhật
b: Xét tứ giác ABMD có
AD//BM
AD=BM
=>ABMD là hình bình hành

45 và 72 là 62,5%
15,3 và 30 là 51%
16 và 80 là 20%
8,4 và 56 là 15%
1/ 45:72=0,625=62,5% 2/ 15,3:30=0,51=51% 3/ 16:80=0,2=20% 4/ 8,4:56=0,15=15%

B16:
Biểu thức C là tích của 100 phân số nhỏ hơn 1 , trong đó các tử đều lẽ , các mẫu đều chẵn . Ta đưa ra biểu thức trung gian là một tích các phân số mà tử số các phân số đều chẵn và mẫu số các phân số đều lẽ . Thêm 1 vào tử và mẫu của mỗi phân số của A , giá trị mỗi phân số tăng lên , do đó:
ta có:
\(A< \dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}.....\dfrac{199}{200}\left(1\right)\)
\(A< \dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}....\dfrac{200}{201}\left(2\right)\)
Nhân (1) vs (2) theo từng vế ta được:
\(A^2< \left(\dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}.....\dfrac{199}{200}\right).\left(\dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}....\dfrac{200}{201}\right)\)
Vế phải của bđt trên bằng \(\dfrac{1}{201}\)
Vậy \(A^2< \dfrac{1}{201}\left(đpcm\right)\)
15.
\(A=\dfrac{1}{4}+\dfrac{1}{4^2}+...+\dfrac{1}{4^7}\)
\(4A=1+\dfrac{1}{4}+...+\dfrac{1}{4^6}\)
\(\Rightarrow4A-A=1-\dfrac{1}{4^7}\)
\(\Rightarrow3A=1-\dfrac{1}{4^7}\)
\(\Rightarrow A=\dfrac{1}{3}\left(1-\dfrac{1}{4^7}\right)\)
\(B=\dfrac{8}{9}.\dfrac{15}{16}...\dfrac{2499}{2500}=\dfrac{2.4}{3^2}.\dfrac{3.5}{4^2}...\dfrac{49.51}{50^2}\)
\(B=\dfrac{2.3...49}{3.4...50}.\dfrac{4.5...51}{3.4...50}=\dfrac{2}{50}.\dfrac{51}{3}=\dfrac{17}{25}\)

Bài 16:
a: Xét ΔOEH và ΔOFH có
OE=OF
\(\widehat{EOH}=\widehat{FOH}\)
OH chung
Do đó: ΔOEH=ΔOFH

Bài 16:
1) \(x^2+4x+4=\left(x+2\right)^2\)
2) \(x^2+6x+9=\left(x+3\right)^2\)
3) \(4x^2+4x+1=\left(2x+1\right)^2\)
4) \(9+12x+4x^2=\left(2x+3\right)^2\)
5) \(x^2-2x+1=\left(x-1\right)^2\)
6) \(x^2-8x+16=\left(x-4\right)^2\)
7) \(36-12x+x^2=\left(x-6\right)^2\)
8) \(4x^2-12xy+9y^2=\left(2x+3y\right)^2\)
9) \(9x^2-6x+1=\left(3x-1\right)^2\)
10) \(4x^2+12x+9=\left(2x+3\right)^2\)
11) \(x^2+3x+\dfrac{9}{4}=\left(x+\dfrac{3}{2}\right)^2\)
12) \(4x^2-6x+\dfrac{9}{4}=\left(2x-\dfrac{3}{2}\right)^2\)
Bài 16:
1: \(x^2+4x+4=\left(x+2\right)^2\)
2: \(x^2+6x+9=\left(x+3\right)^2\)
3: \(4x^2+4x+1=\left(2x+1\right)^2\)
4: \(4x^2+12x+9=\left(2x+3\right)^2\)
5: \(x^2-2x+1=\left(x-1\right)^2\)
6: \(x^2-8x+16=\left(x-4\right)^2\)
7: \(36-12x+x^2=\left(6-x\right)^2\)
8: \(4x^2-12xy+9y^2=\left(2x-3y\right)^2\)

Bài IV:
1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(3\right)\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD tại C
=>AC\(\perp\)DM tại C
Xét ΔADM vuông tại A có AC là đường cao
nên \(MC\cdot MD=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MA^2=MH\cdot MO=MC\cdot MD\)
3: Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{OAM}=90^0\)
\(\widehat{HAI}+\widehat{OIA}=90^0\)(ΔAHI vuông tại H)
mà \(\widehat{OAI}=\widehat{OIA}\)
nên \(\widehat{MAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAM
Xét ΔAHM có AI là phân giác
nên \(\dfrac{HI}{IM}=\dfrac{AH}{AM}\left(5\right)\)
Xét ΔOHA vuông tại H và ΔOAM vuông tại A có
\(\widehat{HOA}\) chung
Do đó: ΔOHA đồng dạng với ΔOAM
=>\(\dfrac{OH}{OA}=\dfrac{HA}{AM}\)
=>\(\dfrac{OH}{OI}=\dfrac{AH}{AM}\left(6\right)\)
Từ (5) và (6) suy ra \(\dfrac{OH}{OI}=\dfrac{IH}{IM}\)
=>\(HO\cdot IM=IO\cdot IH\)





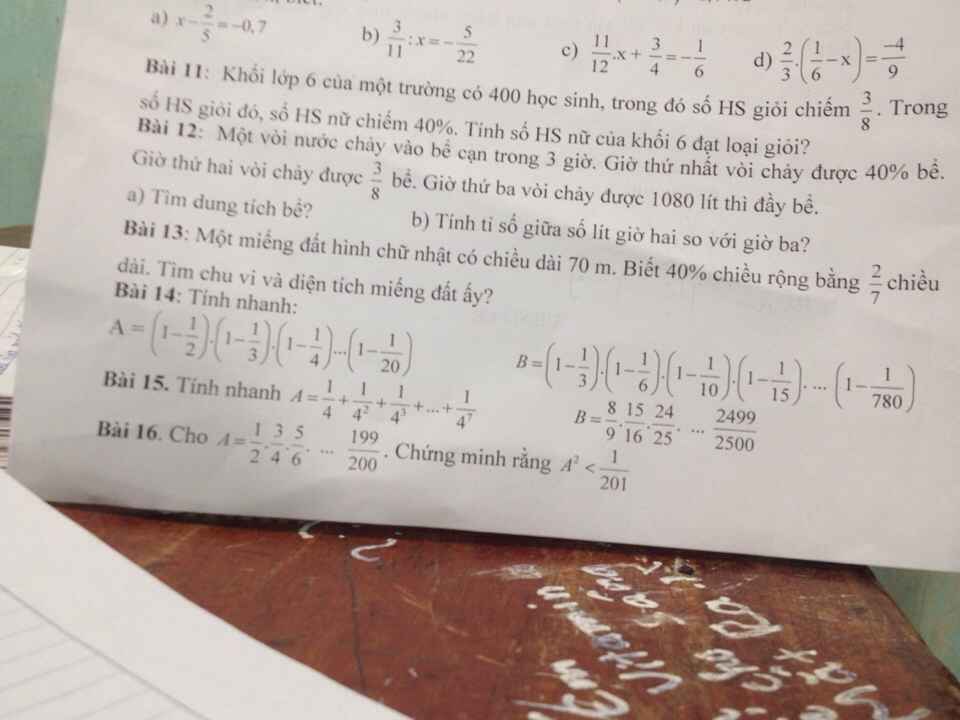



a, sơ đồ dễ vẽ thôi bạn tự vẽ nhé
b, R1 nt(R2//R3)
\(\Rightarrow Im=I1=I23=\dfrac{U}{Rtd}=\dfrac{27}{R1+\dfrac{R2R3}{R2+R3}}=1,8A\)
\(\Rightarrow U23=U2=U3=I23\left(\dfrac{R2R3}{R2+R3}\right)=10,8V\)
\(\Rightarrow\left\{{}\begin{matrix}I1=1,8A\\I2=\dfrac{10,8}{R2}=1,08A\\I3=I1-I2=0,72A\end{matrix}\right.\)