\(a.\)

Xét \(\Delta ADE\) và \(\Delta ABC\) có :

\(AD=AB\) \(\left(gt\right)\)

\(\widehat{DAE}=\widehat{BAC}\left(=90^0\right)\)

\(AE=AC\) \(\left(gt\right)\)

Do đó : \(\Delta ADE=\Delta ABC\left(c-g-c\right)\)

\(\Rightarrow DE=BC\) ( hai cạnh tương ứng )

\(b.\)

Ta có :

\(\widehat{ADE}=\widehat{CDN}\) ( hai góc đối đỉnh )

\(\widehat{C}=\widehat{E}\) ( vì \(\Delta ADE=\Delta ABC\) )

\(\Rightarrow\widehat{N}=\widehat{A}\left(90^0\right)\)

Hay \(DE\perp BC\)

Vậy \(DE\perp BC\)

còn phần c

bạn nào giúp mk vẽ hình đc không

Xét ΔADE và ΔABC có :
AD = AB (gt)

góc DAE =góc BAC = 90 độ
AE = AC (gt)
Do đó : ΔADE = ΔABC(c − g − c)
⇒ DE = BC ( hai cạnh tương ứng )
b.
Ta có :
góc ADE =góc CDN ( hai góc đối đỉnh )
góc C= góc E
( vì ΔADE = ΔABC )
⇒ góc N = góc A 90đọ
Hay DE ⊥ BC
Vậy DE ⊥ BC

a: Xét ΔABC vuông tại A và ΔADE vuông tại A có

AB=AD

AC=AE

Do đó: ΔABC=ΔADE

b: Xét ΔAMD và ΔANB có

AM=AN

MD=NB

AD=AB

Do đó: ΔAMD=ΔANB

Tham khảo:

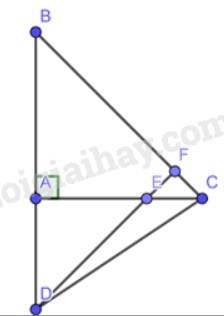
a) Vì tam giác ABC vuông cân tại A

\( \Rightarrow \) \(\widehat B = \widehat C = {45^o}\)(2 góc ở đáy bằng nhau)

Xét tam giác AED có :

AE = AD

AC vuông góc với AB

\( \Rightarrow \) Tam giác AED vuông cân tại A

\( \Rightarrow \widehat {ADE} = \widehat {AED} = {45^o}\)

Mà \(\widehat {AED};\widehat {CEF}\)là 2 góc đối đỉnh \( \Rightarrow \widehat {AED} = \widehat {CEF} = {45^o}\)

Xét tam giác CEF áp dụng định lí tổng 3 góc trong tam giác ta có :

\( \Rightarrow \widehat F + \widehat C + \widehat E = {180^o}\)

\( \Rightarrow \widehat F = {180^o} - {45^o} - {45^o} = {90^o} \Rightarrow EF \bot BC \Rightarrow DE \bot BC\)

b) Vì DE vuông góc với BC \( \Rightarrow \) DE là đường cao của tam giác BCD

Vì AC cắt DE tại E nên E là trực tâm tam giác BCD (Do AC cũng là đường cao của tam giác BCD)

\( \Rightarrow \)BE cùng là đường cao của tam giác BCD (định lí 3 đường cao trong tam giác đi qua trực tâm)

\( \Rightarrow \)BE vuông góc với DC

1) Xét ΔCAB vuông tại A và ΔEAD vuông tại A có 

AB=AD(gt)

AC=AE(gt)

Do đó: ΔCAB=ΔEAD(hai cạnh góc vuông)

Suy ra: BC=DE(hai cạnh tương ứng)

2) Xét ΔABD có AB=AD(gt)

nên ΔABD cân tại A(Định nghĩa tam giác cân)

Xét ΔABD cân tại A có \(\widehat{BAD}=90^0\)(gt)

nên ΔABD vuông cân tại A(Định nghĩa tam giác vuông cân)

a: Gọi giao của DE và BC là H

góc HDB+góc HBD=45+45=90 độ

=>DE vuông góc BC

b: Xet ΔABC có

DE,CA là đường cao

DE cắt CA tại E

=>E là trực tâm

=>BE vuông góc DC

Dạ em cảm ơn