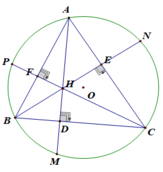
Cho tam giác ABC nhọn nội tiếp (O) các đường cao AD, BE, CF cắt đường tròn thứ tự tại M,N,K. Chứng minh rằng: \(\dfrac{AM }{AD}+\dfrac{BN}{BE}+\dfrac{CK}{CF}=4\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu hỏi của toán khó mới hay - Toán lớp 9 - Học toán với OnlineMath
Ta có SABC=\(\dfrac{AD.BC}{2}\)
Tứ giác ABMC có AM⊥BC⇒SABMC=\(\dfrac{AM.BC}{2}\)
Suy ra \(\dfrac{S_{ABMC}}{S_{ABC}}=\dfrac{AM}{AD}\)
Chứng minh tương tự: \(\dfrac{S_{ABCN}}{S_{ABC}}=\dfrac{BN}{BE}\)
\(\dfrac{S_{ACBK}}{S_{ABC}}=\dfrac{CK}{CF}\)
Vậy \(\dfrac{AM}{AD}+\dfrac{BN}{BE}+\dfrac{CK}{CF}=\dfrac{S_{ABMC}+S_{ABCN}+S_{ACBK}}{S_{ABC}}=\dfrac{S_{ABC}+S_{BMC}+S_{ABC}+S_{ANC}+S_{ABC}+S_{ABK}}{S_{ABC}}=3+\dfrac{S_{BMC}+S_{ANC}+S_{AKB}}{S_{ABC}}\)(1)
Gọi H là giao điểm của AD,BE,CF ta có
\(\widehat{MBD}=\widehat{MBC}=\widehat{MAC}\)(cùng chắn cung MC)=\(\widehat{EAH}=90^0-\widehat{AHE}=90^0-\widehat{BHD}=\widehat{HBD}\)
Lại có BD là cạnh chung
\(\widehat{BDH}=\widehat{BDM}=90^0\)
Suy ra △BHD=△BMD(cạnh huyền, góc nhọn)\(\Rightarrow HD=MD\Rightarrow S_{BMC}=\dfrac{MD.BC}{2}=\dfrac{HD.BC}{2}=S_{BHC}\)
Chứng minh tương tự: \(S_{ANC}=S_{AHC}\)
\(S_{AKB}=S_{AHB}\)
Vậy \(\dfrac{AM}{AD}+\dfrac{BN}{BE}+\dfrac{CK}{CF}=3+\dfrac{S_{BMC}+S_{AKB}+S_{ANC}}{S_{ABC}}=3+\dfrac{S_{BHC}+S_{ABH}+S_{AHC}}{S_{ABC}}=3+\dfrac{S_{ABC}}{S_{ABC}}=3+1=4\)
Vậy \(\dfrac{AM}{AD}+\dfrac{BN}{BE}+\dfrac{CK}{CF}=4\)

a) Ta thấy \(\widehat{BAM}=\widehat{BCM}\) (Cùng phụ với góc \(\widehat{ABC}\) )
Vậy nên \(\widebat{KB}=\widebat{MB}\), suy ra \(\widehat{KCB}=\widehat{MCB}\) (Hai góc nội tiếp chắn các cung bằng nhau)
Gọi giao điểm của ba đường cao là H.
Xét tam giác MHC có CD là đường cao đồng thời là phân giác nên tam giác MHC cân tại C.
Vậy thì CD cũng là trung tuyến hay DM = DH.
Ta có \(\frac{AM}{AD}=\frac{AD+DM}{AD}=1+\frac{DM}{AD}=1+\frac{DH}{AD}\)
Tương tự \(\frac{BN}{BE}=1+\frac{HE}{BE};\frac{CK}{CF}=1+\frac{FH}{CF}\)
Ta có \(\frac{AM}{AD}+\frac{BN}{BE}+\frac{CK}{CF}=3+\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}\)
Lại thấy rằng \(\frac{DH}{AD}=\frac{S_{HBC}}{S_{ABC}};\frac{HE}{BE}=\frac{S_{HAC}}{S_{ABC}};\frac{HF}{CF}=\frac{S_{HAB}}{S_{ABC}}\)
nên \(\frac{HD}{AD}+\frac{HE}{BE}+\frac{HF}{CF}=\frac{S_{HBC}+S_{HAC}+S_{HAB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\)
Vậy thì \(\frac{AM}{AD}+\frac{BN}{BE}+\frac{CK}{CF}=3+1=4\)

Lời giải:
\(S_{ABC}=\frac{AD.BC}{2}; S_{ABMC}=\frac{AM.BC}{2}\)
\(\Rightarrow \frac{S_{ABMC}}{S_{ABC}}=\frac{AM}{AD}\)
Hoàn toàn TT: \(\frac{S_{ABCN}}{S_{ABC}}=\frac{BN}{BE}; \frac{S_{ACBK}}{S_{ABC}}=\frac{CK}{CF}\)
Do đó:
\(\frac{AM}{AD}+\frac{BN}{BE}+\frac{CK}{CF}=\frac{S_{ABMC}+S_{ABCN}+S_{ACBK}}{S_{ABC}}\)
\(=\frac{S_{ABC}+S_{BMC}+S_{ABC}+S_{ANC}+S_{ABC}+S_{AKB}}{S_{ABC}}=3+\frac{S_{BMC}+S_{ANC}+S_{AKB}}{S_{ABC}}(*)\)
Lại có:
\(\widehat{MBD}=\widehat{MBC}=\widehat{MAC}\) (góc nội tiếp cùng chắn cung MC)
\(=\widehat{HAE}=90^0-\widehat{AHE}=90^0-\widehat{BHD}=\widehat{HBD}\)
Xét tam giác $HBD$ và $MBD$ có:
\(\left\{\begin{matrix} \widehat{MBD}=\widehat{HBD}\\ \widehat{BDH}=\widehat{BDM}=90^0\end{matrix}\right.\) \(\Rightarrow \triangle HBD\sim \triangle MBD\)
\(\Rightarrow \frac{HD}{BD}=\frac{MD}{BD}\Rightarrow HD=MD\)
\(\Rightarrow S_{BHC}=\frac{HD.BC}{2}=\frac{MD.BC}{2}=S_{BMC}\)
Hoàn toàn TT: \(S_{AHC}=S_{ANC}; S_{AHB}=S_{AKB}\)
\(\Rightarrow S_{BMC}+S_{ANC}+S_{AKB}=S_{BHC}+S_{AHC}+S_{AHB}=S_{ABC}(**)\)
Từ \((1);(2)\Rightarrow \frac{AM}{AD}+\frac{BN}{BE}+\frac{CK}{CF}=3+\frac{S_{ABC}}{S_{ABC}}=4\) (đpcm)

a) Xét tứ giác CEHD có:
∠(CED) = 90 0 (do BE là đường cao)
∠(HDC) = 90 0 (do AD là đường cao)
⇒ ∠(CED) + ∠(HDC) = 180 0
Mà ∠(CED) và ∠(HDC) là 2 góc đối của tứ giác CEHD nên CEHD là tứ giác nội tiếp
.