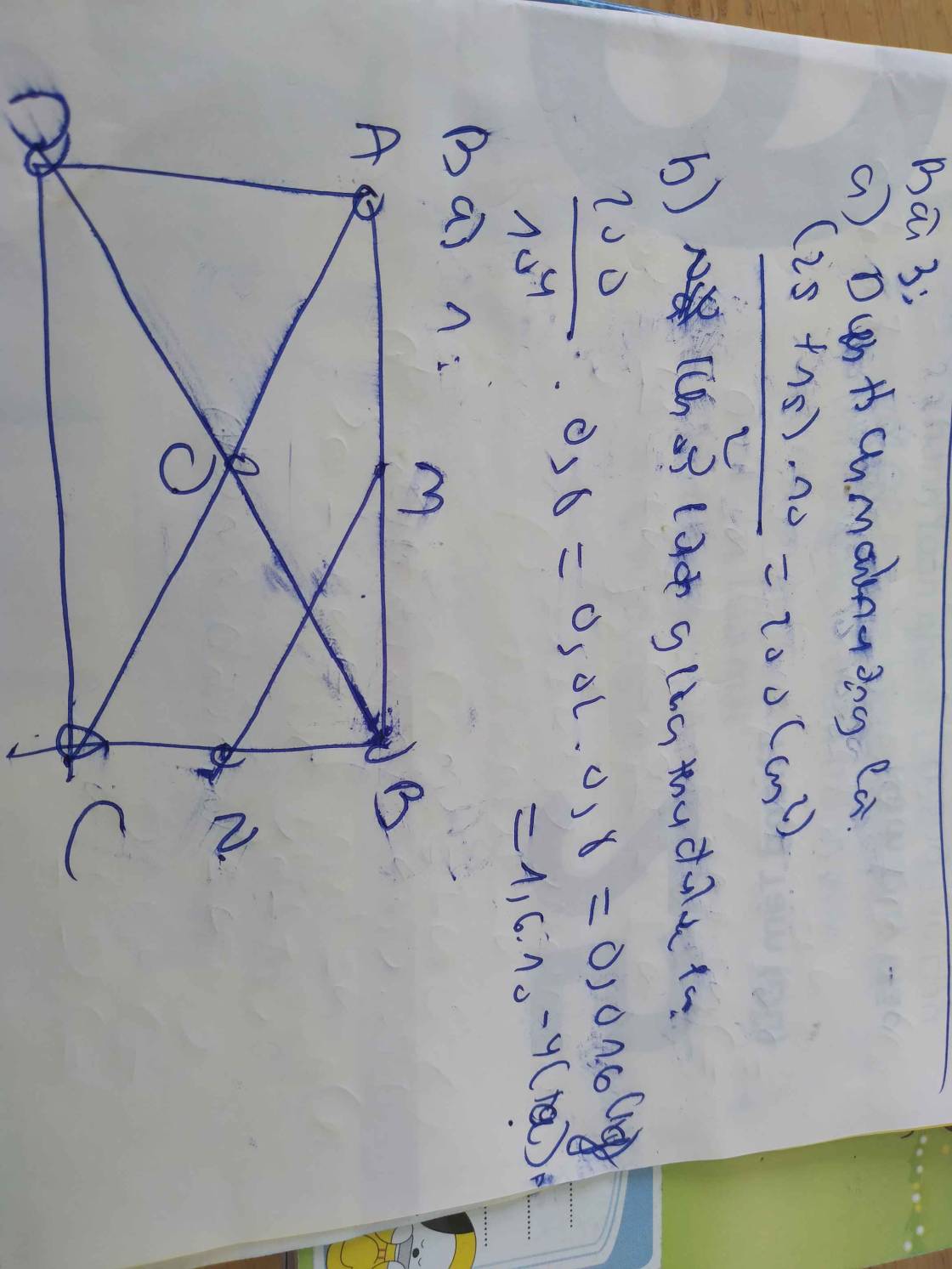
Tự vẽ hình nhá :))

*Nối MC

Số đo cạnh AM là : 12 : 2 = 6 (dm)

Vì 12 dm2 = 1 x 12 mà nửa AB đã là 6 dm => Chiều dài = 12,chiều rộng là 1

Diện tích hình tam giác AMC là : 6 x 1 : 2 = 3 dm2

Đ/s :....

( Mình ko chắc lắm )

Vì diện tích hình chữ nhật ABCD là 12dm2 nên thoả mãn điều kiện chiều dài là 3dm, chiều rộng là 4dm.

Vậy độ dài đáy hình tam giác AMC là:

4: 2 = 2 (dm)

Diện tích hình tam giác  AMC là: 2* 3/2= 3 (dm2)

Đ/s: 3dm2

Ta có:         *    \(\frac{S_{\Delta ADE}}{S_{\Delta ADB}}=\frac{1}{2}\)  mà \(\frac{S_{\Delta ADB}}{S_{ABCD}}=\frac{1}{2}\)  suy ra   \(\frac{S_{\Delta ADE}}{S_{ABCD}}=\frac{1}{4}\)
                   *   \(\frac{S_{\Delta DCM}}{S_{\Delta DCB}}=\frac{1}{2}\) mà \(\frac{S_{\Delta CDB}}{S_{ABCD}}=\frac{1}{2}\)  suy ra \(\frac{S_{\Delta DCM}}{S_{ABCD}}=\frac{1}{4}\)
                   *   \(\frac{S_{\Delta EBM}}{S_{\Delta EBC}}=\frac{1}{2}\)  mà  \(\frac{S_{\Delta EBC}}{S_{\Delta ABC}}=\frac{1}{2}\)  suy ra    \(\frac{S_{\Delta EBM}}{S_{\Delta ABC}}=\frac{1}{4}\) 
                                             tuy nhiên  \(\frac{S_{\Delta EBC}}{S_{ABCD}}=\frac{1}{4}\)  suy ra \(\frac{S_{\Delta EBM}}{S_{ABCM}}=\frac{1}{8}\)

Ta lại có:    \(\frac{S_{\Delta DEM}}{S_{ABCD}}=S_{ABCD}-\left(S_{\Delta ADE}+S_{\Delta EBM}+S_{\Delta DCM}\right)=1-\left(\frac{1}{4}+\frac{1}{4}+\frac{1}{8}\right)=\frac{3}{8}\)
    \(\Rightarrow\)   \(S_{ABCD}=S_{\Delta DEM}\div\frac{3}{8}=6\times\frac{8}{3}=16\left(cm^2\right)\)

ai trả lời đúng

cho 1 cho ai trả lời đúng

a: BC=3/4*30=22,5cm

S CBA=1/2*22,5*30=337,5cm²

=>S AMC=1/2*337,5=168,75cm²

b: S ADC=1/2*22,5*30=337,5cm²

=>S AMCD=337,5+168,75=506,25cm²