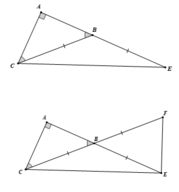
Cho tam giác ABC nhọn,vẽ về phía ngoài các tam giác ABD,ACE,BCF.Gọi M là giao điểm của DC và BE.
a.C/minh BE=CD
b.Tính góc BMC
c.C/minh MA+MB=MD
d.C/minh AF,BE,CD đồng quy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Xét \(\Delta ACD\)và \(\Delta AEB\)có:
AE=AB (vì \(\Delta ACE\)đều)
\(\widehat{CAD}=\widehat{BAE}\left(=60^o+\widehat{BAC}\right)\)
AD=AB (vì \(\Delta ABD\)đều)
\(\Rightarrow\Delta ACD=\Delta AEB\left(c.g.c\right)\)
\(\Rightarrow CD=EB\)
2 dễ, tự làm.

a:
góc BAE=góc BAC+góc CAE=góc BAC+60 độ
góc CAD=góc CAB+góc BAD=góc BAC+60 độ
=>góc BAE=góc CAD
Xét ΔABE và ΔADC có
AB=AD
góc BAE=góc DAC
AE=AC
=>ΔABE=ΔADC
b: ΔABE=ΔADC
=>góc ABE=góc ADC
=>góc ABM=góc ADM
Xét tứ giác ADBM có
góc ABM=góc ADM
=>ADBM là tứ giác nội tiếp
=>góc DMB=góc DAB=60 độ
góc DMB+góc BMC=180 độ(kề bù)
=>góc BMC=180-60=120 độ

Xét tam giác ADC và tam giác AEB có:
AD = AB(giả thiết)
\(\widehat{DAC}=\widehat{BAE}\)(\(=60^0+\widehat{BAC}\))
AC = AE( giả thiết)
\(\Rightarrow\)tam giác ADC = tam giác ABE (c-g-c)
\(\Rightarrow\widehat{ADC}=\widehat{ABE}\)(2 góc tương ứng)
Xét tam giác ADI và tam giác BIM có:
\(\widehat{ADI}+\widehat{AIM}+\widehat{DAI}=\widehat{IBM}+\widehat{BIM}+\widehat{IMB}=180^0\)(theo định lí tổng 3 góc của tam giác)
Mà \(\widehat{ADI}=\widehat{IBM}\)(chứng minh trên)
\(\widehat{AID}=\widehat{BIM}\)(2 góc đối đỉnh)
\(\Rightarrow\widehat{DAI}=\widehat{IMB}\)
Mà \(\widehat{DAI}=60^0\)
\(\Rightarrow\widehat{IMB}=60^0\)
Ta có: \(\widehat{IMB}+\widehat{BMC}=180^0\)(2 góc kề bù)
\(\Rightarrow60^0+\widehat{BMC}=180^0\)
\(\Rightarrow\widehat{BMC}=180^0-60^0=120^0\)
Vậy \(\widehat{BMC}=120^0\)(ĐPCM)
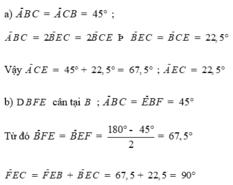
a, Xét tam giác ABE và tam giác ADC có:
AB = AD
góc BAE = góc DAC
AE=AC
==> tam giacs ABE = tam giác ADC ( c.g.c )
(bạn coi lại hộ mình nha xem mình sai chỗ nào)
chúc bạn học tốt!
Nhân ơi đúng rồi nhưng bạn làm thiếu nhé,trước tiên phải c/minh 2 góc bằng nhau đã,nhg dù gì cũng cảm ơn cậu