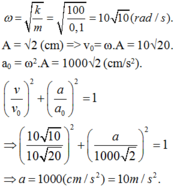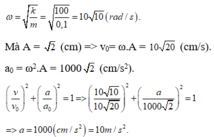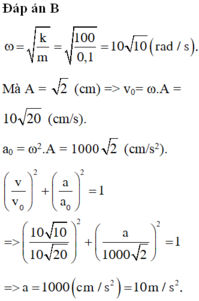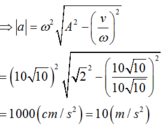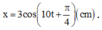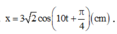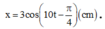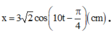Bài 5. Con lắc lò xo nằm ngang có khối lượng 100g, treo vào lò xo có độ cứng 40N/m. Chọn gốc thời gian là lúc vật có li độ 2cm và đang chuyển động với vận tốc 40√ cm/s. a. Viết phương trình dao động b. Tính lực đàn hồi cực đại của lò xo
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
24 tháng 4 2019
Chọn đáp án A.
ω = k m = 100 0 , 1 = 10 10 ( r a d / s ) .
Mà A = 2 (cm) => v 0 = ω . A = 10 2 c m / s .
a 0 = ω 2 . A = 1000 2 c m / s 2
v v 0 2 + a a 0 2 = 1 ⇒ 10 10 10 20 2 + a 1000 2 2 = 1
⇒ a = 1000 ( c m / s 2 ) = 10 m / s 2 .
15 tháng 7 2016
Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)
