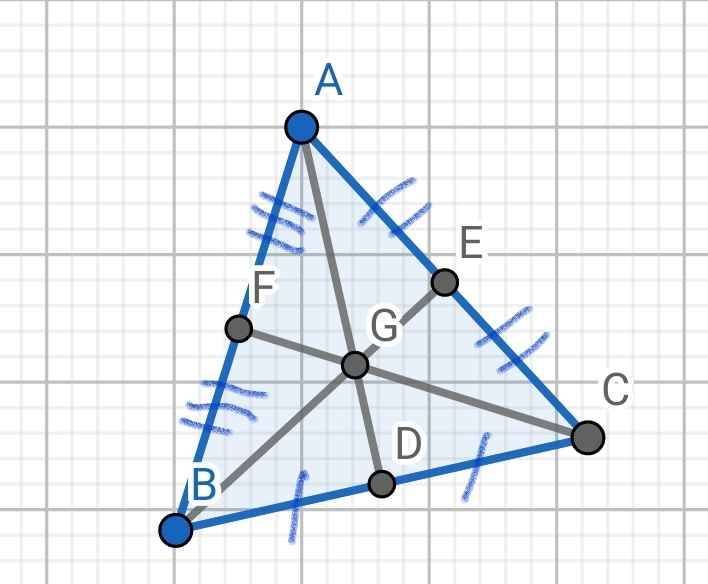
Tam giác ABC có BC = 20cm. Trung tuyến AD,BE,CF cắt nhau tại G
a) chứng minh: BE+CF>30. b) gọi M,N là trung điểm GB,GC. chứng minh AD,BN,CM đồng quy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC có
AD,BE,CF là trung tuyến
AD,BE,CF cắt nhau tai G
=>G là trọng tâm
=>BG=2/3BE=2BM và CG=2/3CF=2CN
=>M,N lần lượt là trung điểm của GB,GC
=>GD,CM,BN đồng quy
=>AD,CM,BN đồng quy

Câu hỏi của ✎﹏ Ƈøoȴ _ Ǥɩ®ʆ _☜♥☞ ✓ - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo nhé!

a) Do ∆ABC đều
⇒ AB = AC = BC và ∠A = ∠B = ∠C = 60⁰
Do AD, BE, CF là ba đường trung tuyến
⇒ F, E, D lần lượt là trung điểm của AB, AC, BC
⇒ AF = BF = AE = CE = BD = CD
Xét ∆BEC và ∆CFB có:
CE = BF (cmt)
BC chung
∠BCE = ∠CBF = 60⁰
⇒ ∆BEC = ∆CBF (c-g-c)
⇒ BE = CF (hai cạnh tương ứng) (1)
Xét ∆ADC và ∆CFA có:
AC chung
CD = AF (cmt)
∠ACD = ∠CAF = 60⁰
⇒ ∆ADC = ∆CFA (c-g-c)
⇒ AD = CF (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ AD = BE = CF (3)
b) Do AD là đường trung tuyến ứng với đỉnh A
⇒ AG = 2/3 AD (4)
Do BE là đường trung tuyến ứng với đỉnh B
⇒ BG = 2/3 BE (5)
Do CF là đường trung tuyến ứng với đỉnh C
⇒ CG = 2/3 CF (6)
Từ (3), (4), (5), (6) ⇒ AG = BG = CG

-△ABC có: G là trọng tâm; AD, BE, CF là các trung tuyến:
\(\Rightarrow BG=\dfrac{2}{3}BE;CG=\dfrac{2}{3}CF\)
\(\Rightarrow BG=2BM;CG=2CN\)
\(\Rightarrow\)M là trung điểm BG ; N là trung điểm CG.
-△BCG có: CM là trung tuyến (N là trung điểm CG) ; BN là trung tuyến
(M là trung điểm BG) ; GD là trung tuyến (D là trung điểm BC)
\(\Rightarrow\)AD; BN; CM đồng quy.