Cho tan giác ABC vuông tại A, đường cao AH. BH=4cm,CH=9cm:
- Chứng minh AB^2 =BH x BC
- Tính AB,AC
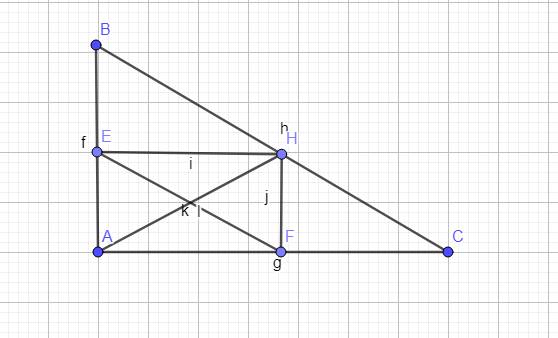
- Đường phân giác BD của góc B cắt AH tại E(D thuộc AC). Tỉnh tỉ sô \(\frac{S_{EBH}}{S_{DAB}}\)
- Chứng minh \(\frac{AB}{EH}\)= \(\frac{BC}{DA}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABC và tam giác HBA có
Góc BAC = góc BHA = 90độ
góc B chung
=)tg ABC đồng dạng với tg HBA
=)AB/BH = BC/AB (cặp cạnh tương ứng)
=) AB^2 = BH.BC (đpcm)
b) có AB^2 = BH.BC (cmt)
mà BH = 4cm , BC = BH + CH =4+9 = 13cm
=) AB^2 = 4+13 = 17
=) AB = \(\sqrt{17}\)cm
xét tg vuông ABC áp dụng định lý Py-ta-go ta có
AB^2 + AC^2 = BC^2
thay số: \(\sqrt{17}^2\)+ AC^2 = 13^2
=) AC =\(2\sqrt{38}\)cm
vậy nhé chứ ý c mik thấy đầu bài sai sai

1 phần thôi nhé
Nối BE, Gọi P là giao điểm của AD với BE.
Áp dụng định lí Ceva cho tam giác ABE => AH/HE=BP/PE=> HP//AB(1).
Từ (1)=> Tam giác AHP cân tại H=> AH=HP.(2)
Ta cần chứng minh AD//CE <=> DP//CE <=> BD/BC=BP/BE <=> BD/BC=1-(EP/BE).(3)
Mà EP/BE=HP/AB (do (1))=> EP/BE= AH/AB=HD/DB (do (2) và tc phân giác). (4)
Khi đó (3)<=> BD/BC=1-(HD/DB) hay (BD/BC)+(HD/DB)=1 <=> BD^2+HD*BC=BC*DB
<=> BD^2+HD*BC= (BD+DC)*BD <=> BD^2+HD*BC= BD^2+BD*DC <=> HD*BC=BD*DC
<=> HD/DB=CD/BC <=> AH/AB=CD/BC. (5)
Chú ý: Ta cm được: CA=CD (biến đổi góc).
Nên (5) <=> AH/AB=CA/BC <=> Tg AHB đồng dạng Tg CAB.( luôn đúng)
=> DpCm.

Ta có: tam giác vuông EBH \(\sim\) tam giác vuông ABC (gt)
=>\(\dfrac{S\Delta EBH}{S\Delta ABC}=\left(\dfrac{BH}{BC}\right)^2\Rightarrow\dfrac{\sqrt{S\Delta EBH}}{\sqrt{S\Delta ABC}}=\dfrac{BH}{BC}\left(1\right)\)
Ta có tam giác vuông FHC \(\sim\) tam giác vuông ABC (g.g)
=>\(\dfrac{S\Delta FHC}{S\Delta ABC}=\left(\dfrac{HC}{BC}\right)^2\Rightarrow\dfrac{\sqrt{S\Delta FHC}}{\sqrt{S\Delta ABC}}=\dfrac{HC}{BC}\left(2\right)\)
\(\)Từ (1)và (2) =>\(\dfrac{\sqrt{S\Delta EBH}+\sqrt{S\Delta FHC}}{\sqrt{S\Delta ABC}}=\dfrac{HB+HC}{BC}=\dfrac{BC}{BC}=1\)
Vậy \(\sqrt{S\Delta_{EBH}}+\sqrt{S\Delta_{FHC}}=\sqrt{S\Delta_{ABC}}\left(đpcm\right)\)
chucbanhoctot!
thực ra ở đây ko thể c/m đc yêu cầu của bạn đâu, cần phải có AEHF là hcn mới ra cơ ạ

Cô hướng dẫn nhé.
a. Kẻ \(DK\perp BC.\)
Khi đó ta thấy \(IA=IK;DA=DK.\)Lại có \(\Delta HIK\sim\Delta KDC\left(g-g\right)\Rightarrow\frac{IH}{KD}=\frac{IK}{DC}\Rightarrow\frac{IH}{IK}=\frac{KD}{DC}\Rightarrow\frac{IH}{IA}=\frac{DA}{DC}\)
b. Ta có \(BE.AB=BH^2;CF.AC=HC^2\Rightarrow BE.AB.CF.AC=HB^2.HC^2=AH^4\)
\(\Rightarrow BE.CF\left(AB.AC\right)=AH^4\Rightarrow BE.CF.AH.BC=AH^4\Rightarrow BE.CF.BC=AH^3\)
c. Tính \(BE\Rightarrow AE;CF\Rightarrow AC\Rightarrow S_{EHF}\)