a=x⁴-2223x³+2223x²-2223x+2223

=x³(x-2223)+x(x-2223)+2222x²+2003(*)

thay x=2222,ta co:

(*)<=>-2222³-2222+2222³+2223=1

dung thi chon nha

dễ mà                                 

Thay x = -1 và đa thức, ta có:

(-1)2 + (-1)4 + (-1)6 + … + (-1)100 =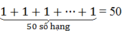 

Vậy giá trị đa thức bằng 50 tại x = -1.

f(-1)= 1+(-1)+(-1)²+...+(-1)¹⁰⁰

=1+(-1)+1+...+1

=1+0

=1

A(x)=F(x)-G(x)

=1+x+x^2+...+x^100-x^2-x^4-...-x^100

=1+x+x^3+...+x^99

Số số lẻ từ 1 đến 99 là (99-1):2+1=50(số)

A(-1)=1+(-1)+(-1)^3+...+(-1)^99

=1-50*1=1-50=-49

a: \(f\left(-2\right)=5\cdot4-8-8=4\)

b: \(f\left(x\right)+g\left(x\right)=6x^2+2x-8\)

c: Đặt G(x)=0

=>x(x-2)=0

=>x=0 hoặc x=2

\(x^4-2015x^3+2015x^2-2015x+2015\)

\(=x^4-\left(x+1\right)x^3+\left(x+1\right)x^2-\left(x+1\right)x+x+1\)(vì x=2014 nên 2015=x+1)

\(=x^4-x^4-x^3+x^3+x^2-x^2-x+x+1\)

\(=1\)

\(f_{\left(x\right)}=x^6-2002x^5+2002x^4-2002x^3+2002x^2-2002x+2006\)

\(=x^6-\left(x+1\right)x^5+\left(x+1\right)x^4-\left(x+1\right)x^3+\left(x+1\right)x^2-\left(x+1\right)x+x+5\)

\(=x^6-x^6-x^5+x^5+x^4-x^4-x^3+x^3+x^2-x^2-x+x+5\)

\(=5\)

Vậy \(f_{\left(x\right)}=5\)Tại x = 2001

Lạ OLM ghê làm sai mà vẫn được k ???

Ta có : x=2001 \(\Rightarrow\)x+1=2002

\(F\left(x\right)=x^6-\left(x-1\right).x^5+\left(x-1\right).x^4-\left(x-1\right).x^3+\left(x-1\right).x^2-\left(x-1\right).x+2006\)

\(F\left(x\right)=x^6-x^6-x^5+x^5+x^4-x^4-x^3+x^3+x^2-x^2-x+2006\)

\(F\left(2001\right)=-2001+2006=5\)