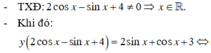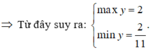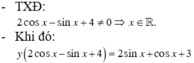tìm GTLN và GTNN của hàm số \(\sin^4x+cos^2x+2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2.
$y=\sin ^4x+\cos ^4x=(\sin ^2x+\cos ^2x)^2-2\sin ^2x\cos ^2x$
$=1-\frac{1}{2}(2\sin x\cos x)^2=1-\frac{1}{2}\sin ^22x$
Vì: $0\leq \sin ^22x\leq 1$
$\Rightarrow 1\geq 1-\frac{1}{2}\sin ^22x\geq \frac{1}{2}$
Vậy $y_{\max}=1; y_{\min}=\frac{1}{2}$
3.
$0\leq |\sin x|\leq 1$
$\Rightarrow 3\geq 3-2|\sin x|\geq 1$
Vậy $y_{\min}=1; y_{\max}=3$

a.
\(-1\le sin\left(1-x^2\right)\le1\)
\(\Rightarrow y_{min}=-1\) khi \(1-x^2=-\dfrac{\pi}{2}+k2\pi\) \(\Rightarrow x^2=\dfrac{\pi}{2}+1+k2\pi\) (\(k\ge0\))
\(y_{max}=1\) khi \(1-x^2=\dfrac{\pi}{2}+k2\pi\Rightarrow x^2=1-\dfrac{\pi}{2}+k2\pi\) (\(k\ge1\))
b.
Đặt \(\sqrt{2-x^2}=t\Rightarrow t\in\left[0;\sqrt{2}\right]\subset\left[0;\pi\right]\)
\(y=cost\) nghịch biến trên \(\left[0;\pi\right]\Rightarrow\) nghịch biến trên \(\left[0;\sqrt{2}\right]\)
\(\Rightarrow y_{max}=y\left(0\right)=cos0=1\) khi \(x^2=2\Rightarrow x=\pm\sqrt{2}\)
\(y_{min}=y\left(\sqrt{2}\right)=cos\sqrt{2}\) khi \(x=0\)