TÌM GIÁ TRỊ NHỎ NHẤT G(X)= 16X4 - 72X2 + 90
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Xét hàm số f(x) = x 3 + 3 x 2 − 72x + 90 trên đoạn [-5;5]
f′(x) =3 x 2 + 6x − 72;
f′(x) = 0 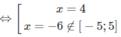
f(−5) = 400; f(5) = −70; f(4) = −86
Ngoài ra, f(x) liên tục trên đoạn [-5;5] và f(−5).f(5) < 0 nên tồn tại x 0 ∈ (−5;5) sao cho f( x 0 ) = 0
Ta có g(x) = |f(x)| ≤ 0 và g( x 0 ) = |f( x 0 )| = 0;
g(−5) = |400| = 400
g(5) = |−70| = 70; g(4) = |f(4)| = |−86| = 86
Vậy min g(x) = g( x 0 ) = 0; max g(x) = g(−5) = 400

Tìm giá trị nhỏ nhất của đa thức g(x)=16x4-72x2+90
Ta có:
g(x)=16x4−72x2+90
=(4x2)2−2.4x2.9+92+9
=(4x2−9)2+9
Với mọi giá trị của x ta có: (4x2−9)2≥0
⇒g(x)=(4x2−9)2+9≥9
Dấu "=" xảy ra khi ⇔(4x2-9)2=0⇔x=± \(\frac{3}{2}\)
Vậy GTNN của đa thức \(g\left(x\right)\)là 9 tại x=\(\pm\frac{3}{2}\)

giá trị tuyệt đối x+10 lớn hơn hoăc bằng 0
=> giá trị tuyệt đối x+10 cộng với 2005
sẽ lớn hơn hoăc bằng 2005 => A lớn hơn hoăc bằng 2005
Dấu bằng xảy ra <=> giá trị tuyệt đối x+10 bằng 0
=> x=-10
Vậy Min B = 2005 <=> x=-10

a, A = /x-1/ + / y+3 / - 7
ta có : /x-1/ >_ 0
/y+3/>_ 0
=> /x-1/ + /y+ 3/ >_ 0
=>/x-1/ +/y+3/ - 7 >_ -7
=> A >_ -7
=> Amin =-7
nhớ tích nha bạn

\(G=\left|x-4\right|+\left|x+6\right|\)
\(G=\left|x-4\right|+\left|-\left(x+6\right)\right|\)
\(G=\left|x-4\right|+\left|-6-x\right|\)
Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\)ta có :
\(G=\left|x-4\right|+\left|-6-x\right|\ge\left|x-4-6-x\right|=\left|-10\right|=10\)
Đẳng thức xảy ra khi \(ab\ge0\)
=> \(\left(x-4\right)\left(-6-x\right)\ge0\)
Xét hai trường hợp :
1/ \(\hept{\begin{cases}x-4\ge0\\-6-x\ge0\end{cases}}\Rightarrow\hept{\begin{cases}x\ge4\\-x\ge6\end{cases}}\Rightarrow\hept{\begin{cases}x\ge4\\x\le-6\end{cases}}\)( loại )
2/ \(\hept{\begin{cases}x-4\le0\\-6-x\le0\end{cases}}\Rightarrow\hept{\begin{cases}x\le4\\-x\le6\end{cases}\Rightarrow}\hept{\begin{cases}x\le4\\x\ge-6\end{cases}}\Rightarrow-6\le x\le4\)
=> GMin = 10 , đạt được khi \(-6\le x\le4\)
\(G=|x-4|+|x+6|=|-\left(x-4\right)|+|x+6|\)
\(=|-x+4|+|x+6|=|4-x|+|x+6|\)
Sử dụng bất đẳng thức \(|a|+|b|\ge|a+b|\)ta có :
\(|4-x|+|x+6|\ge|4-x+x+6|=|10|=10\)
Dấu = xảy ra \(\Leftrightarrow\left(4-x\right)\left(x+6\right)\ge0\Leftrightarrow-6\le x\le4\)
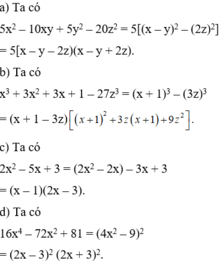
do 16x4 \(\ge\)0
72x2 \(\ge\)0
=> 16x^4 - 72x^2 \(\ge\)0
=> 16x^4 - 72x^2 + 90 \(\ge\)0
hay G(x) \(\ge\)90
GTNN của G(x) = 90
dấu = xảy ra <=> x = 0
có j ko hiểu cứ nt hỏi mình nhé