Giúp với đang cần gấp ạ.Cảm ơn

15 phút = (1/4)giờ

Gọi vận tốc của ca nô khi nước đứng yên là x (km/h). Điều kiện x > 2

Vận tốc ca nô khi xuôi dòng là x + 2 (km/h)

Vận tốc ca nô khi ngược dòng là x – 2 (km/h)

Thời gian ca nô khi xuôi dòng là:

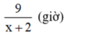
Thời gian ca nô khi ngược dòng là:

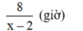
Ta có phương trình:

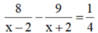
Quy đồng mẫu hai vế:

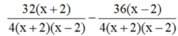
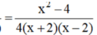
Suy ra:

32x + 64 - 36x + 72 = x2 - 4

⇔ -4x + 136 = x2 - 4

⇔ x2 + 4x - 140 = 0

⇔ (x2 + 4x + 4) - 144 = 0

⇔ (x + 2)2 - 122 = 0

⇔ (x + 14)(x - 10) = 0

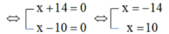
Giá trị x = -14 không thỏa mãn điều kiện

Giá trị x = 10 thỏa mãn điều kiện

Vậy vận tốc của ca nô khi nước yên lặng là 10km/h

Vận tốc xuôi dòng của ca nô là :

21,5 + 2,5 = 24 (km/giờ)

Thời gian ô tô đi hết quãng sông đó là :

84 : 24 = 3,5 (giờ) = 3 giờ 30 phút

3,5 giờ nha

30 phút = 0,5 giờ

Vận tốc và thời gian trên cùng một quảng sông là hai đâị lượng tỉ lệ nghich.

Thời gian về so với thời gian đi :

50 : 40 = 5/4

Thời gian xuôi dòng :

0,5 : (5 - 4) x 4 = 2 giờ

Chiều dài quãng sông AB :

50 x 2 = 100 km

100 km nha

k mình mình k lại cho

Gọi vận tốc riêng của cano là x>3 (km/h)

Thời gian cano xuôi dòng 30km và ngược dòng 28km: \(\dfrac{30}{x+3}+\dfrac{28}{x-3}\) (giờ)

Thời gian cano đi trên 58,5km mặt nước lặng: \(\dfrac{58,5}{x}\) giờ

Theo bài ra ta có pt:

\(\dfrac{30}{x+3}+\dfrac{28}{x-3}=\dfrac{58,5}{x}\)

\(\Leftrightarrow x^2+12x-1053=0\Rightarrow\left[{}\begin{matrix}x=27\\x=-39\left(loại\right)\end{matrix}\right.\)

3 giờ

a: Gọi vận tốc thật của cano là x

Theo đề, ta có: 48/x-2-48/x+2=2/5

=>24/x-2-24/x+2=1/5

=>5[24(x+2)-24(x-2)]=(x+2)(x-2)

=>x^2-4=5(24x+48-24x+48)

=>x^2-4=5*96=480

=>x^2-484=0

=>x=22

b: Thời gian đi từ A đến B là 48/22-2=48/20=2,4(h)

=>Lúc tới B đã 6h15'+2h24'=8h39'

=>Lúc đi từ B về A thì đã 8h39'+20'=8h59'

Thời gian đi từ B về A là 48/22+2=2(h)

=>Khi về tới A đã là: 8h59'+2h=10h59'