Bài giải 

Với mỗi cách chọn 1 nam thì có số cách chọn 2 nữ là:

Em nữ thứ nhất có thể ghép đôi với 5 em còn lại.

Em nữ thứ 2 có thể ghép đôi với 4 em còn lại (trừ em đầu tiên)

Em nữ thứ 3 có thể ghép đôi với 3 em còn lại (trừ em đầu tiên và em thứ 2)

Em nữ thứ 4 có thể ghép đôi với 2 em còn lại (trừ em thứ nhất,thứ 2 và thứ 3)

Em nữ thứ 5 có thể ghép đôi với 1 em còn lại (trừ em thứ nhất, thứ 2 , thứ 3 và thứ 4).

Vậy có số cách ghép 2 nữ là:

                    5 + 4 + 3 + 2 + 1 = 15 (cách)

Vậy cô giáo có số cách chọn 1 nam và 2 nữ vào hát tốp ca nam nữ là:

                   4 x 15 = 60 (cách)

                             Đáp số: 60 cách.

Tự biên tự diễn àk

Số cách chọn các bạn đi lao động là:

Gọi biến cố A: “Chọn mỗi tổ 2 bạn đi lao động, trong đó có đúng 3 bạn nữ”.

Khi đó ta có các TH sau:

+) Tổ 1 có 2 bạn nữ, tổ 2 có 1 bạn nữ và 1 bạn nam có:

+) Tổ 1 có 1 bạn nữ và 1 bạn nam, tổ 2 có 2 bạn nữ có:

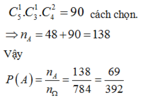
Chọn B.

Chọn B

Chọn mỗi tổ 2 bạn nên số phần tử của không gian mẫu .

Gọi A là biến cố : “Có đúng 3 bạn nữ trong 4 bạn đi lao động”, khi đó

TH1: Chọn 2 nữ tổ I, 1 nữ tổ II, 1 nam tổ II có .

TH2: Chọn 2 nữ tổ II, 1 nữ tổ I, 1 nam tổ I có .

Suy ra .

Xác suất để chọn 4 bạn đi lao động có đúng 3 bạn nữ là .

Cách chọn 2 bạn từ 7 bạn là \(C_{7}^2 \Rightarrow n\left( \Omega  \right) = C_{7}^2 = 21\)

Gọi A là biến cố: “Hai bạn được chọn có một bạn nam và một bạn nữ”.

Cách chọn  một bạn nam là: 3 cách chọn

Cách chọn một bạn nữ là: 4 cách chọn

Theo quy tắc nhân ta có \(n\left( A \right) = 3.4 = 12\)

Vậy xác suất của biến cố A là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{{12}}{{21}} = \frac{4}{7}\).

Chọn A

a) Mỗi cách chọn 3 bạn từ 9 bạn trong tổ một đi trực nhật là một tổ hợp chập 3 của 9. Do đó, số cách cử 3 bạn bất kì đi trực nhật là:

                             \(C_9^3 = \frac{{9!}}{{3!.6!}} = 84\) (cách)

b) Mỗi cách chọn 3 bạn gồm 2 nam và 1 nữ đi trực nhật gồm 2 công đoạn:

          Công đoạn 1: Chọn 2 bạn nam

Mỗi cách chọn 2 bạn nam từ 4 bạn nam đã cho là một tổ hợp chập 2 của 4. Do đó, số cách chọn 2 bạn nam từ 4 bạn nam đã cho là:        \(C_4^2 = \frac{{4!}}{{2!.2!}} = 6\) (cách)

          Công đoạn 2: Chọn 1 bạn nữa trong 5 bạn đã cho, có 5 cách

Áp dụng quy tắc nhân, ta có số các cử 3 bạn đi trực nhật trong đó 2 nam và 1 nữ là:

                             \(6.5 = 30\) (cách)

a. Chọn bất kì 5 học sinh từ 50 học sinh có: \(C_{50}^5\) cách

b. Lớp có 20 học sinh nam. Chọn 5 bạn trong đó có 2 bạn nam (suy ra 3 bạn nữ) đồng nghĩa: chọn 2 nam từ 20 nam và 3 nữ từ 30 nữ

\(\Rightarrow\) Có \(C_{20}^2.C_{30}^3\) cách

c. Số cách chọn 5 bạn toàn là nữ: \(C_{30}^5\) cách

Số cách chọn 5 bạn có ít nhất 1 nam: \(C_{50}^5-C_{30}^5\) cách

2 cách;

2 cách;

2 cách.

k cho mình nhé.