Để có đc 1 đôi giày cần phải lấy ít nhất 2 chiếc giày.

Trong trường hợp xấu nhất là 2 chiếc giày khác màu thì lấy thêm 1 chiếc nữa để chắc chắn có 1 đôi cùng màu.

Vậy cần phải lấy ít nhất 3 chiếc giày

(phần này là phần thêm)

Nếu lấy 3 chiếc giày thì sẽ có 4 trường hợp :

1 . 2 đen và 1 nâu

2. 2 nâu và 1 đen

3. 3 đen

4. 3 nâu

Trong tất cả trường hợp luôn lấy đc 1 đôi giày cùng màu.

Li-ke cho mình nhé mọi người

\(n\left(\Omega\right)=C^4_{10}=210\)

A: "Không chọn được hai chiếc nào tạo thành một đôi".

\(\overline{A}\): "Chọn được ít nhất hai chiếc tạo thành một đôi".

\(n\left(\overline{A}\right)=C^1_5\cdot C_8^2=140\).

\(n\left(A\right)=210-140=70\).

\(P\left(A\right)=\dfrac{70}{210}=\dfrac{1}{3}\).

ta co D=1/2^2+1/3^2+1/4^2+...+1/10^2<1/1.2+1/2.3+1/3.4+...+1/9.10

                                                                =1-1/10

                                                                 =9/10<1

=>D<1

 câu 2 thì tùy theo hên sui

câu 1: Lấy ra 3 chiếc
câu 2:
a, A={1;3;5;7;9;11;13;15;17;19}
b,Tập hợp các số lẻ ko thể chọn ra 5 số có tổng là số chẵn như 30
c,3+7+9+11

Không gian mẫu là kết quả của việc chọn ngẫu nhiên 2 chiếc giày trong số 8 chiếc giày.

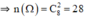
A: “ Chọn được 2 chiếc tạo thành một đôi”

⇒ n(A) = 4 (Vì có 4 đôi).

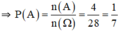
Ta thấy trường hợp xấu nhất là lấy 4 chiếc tất mà trúng phải 4 chiếc của 4 đôi tất
khác nhau.
Do đó khi ta lấy thêm 1 chiếc tất nữa, tổng cộng 4 + 1 = 5 chiếc tất thì chắc chắn có
2 chiếc tất cùng thuộc 1 đôi tất . 

Vậy cần lấy ra ít nhất 5 chiếc bít tất để chắc chắn có 2 chiếc bít tất thuộc cùng một đôi.

5 chiếc

Ba đôi giày có số chiếc giày là :

 3x 2 = 6 (chiếc)

Nếu lấy ra 3 chiếc giày thì trường hợp xấu nhất là 3 chiếc thuộc ba đôi khác nhau. 

Vậy lấy thêm chiếc thứ tư thì chắc chắn nó sẽ là chiếc giày còn lại của một trong ba đôi. Do đó lấy 4 chiếc giày bất kì chắc chắn sẽ có hai chiêc giày cùng một đôi.