Phương trình hoành độ giao điểm: \(x^2-mx-3=0\)

\(ac< 0\Rightarrow\) d luôn cắt (P) tại 2 điểm phân biệt dó hoành độ trái dấu

Theo Viet ta có: \(\left\{{}\begin{matrix}x_A+x_B=m\\x_Ax_B=-3\end{matrix}\right.\)

\(AB^2=\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2\)

\(AB^2=\left(x_A-x_B\right)^2+m^2\left(x_A-x_B\right)^2\) (thay \(y_A=mx_A+3\) và \(y_B\) vào)

\(AB^2=\left(1+m^2\right)\left(x_A-x_B\right)^2\)

\(AB^2=\left(1+m^2\right)\left[\left(x_A+x_B\right)^2-4x_Ax_B\right]\)

\(AB^2=\left(1+m^2\right)\left(m^2+12\right)\)

\(AB^2=m^4+13m^2+12\ge12\) (do \(m^2\ge0\))

\(\Rightarrow AB_{min}=2\sqrt{3}\) khi \(m=0\)

Xét phương trình hoành độ giao điểm:

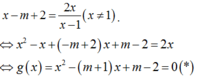
Để đường thẳng d cắt (C) tại 2 điểm phân biệt ⇔ p t *  có 2 nghiệm phân biệt khác 1.

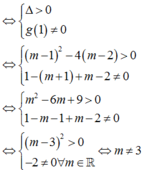
Gọi x A ;   x B  là 2 nghiệm phân biệt của (*), áp dụng định lí Vi-ét ta có: 

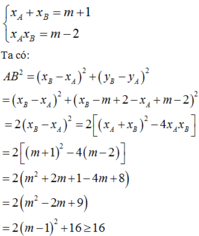
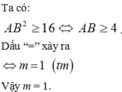
Chọn D.

Đáp án DPhương trình hoành độ gaio điểm của đồ thị (C) và đường thẳng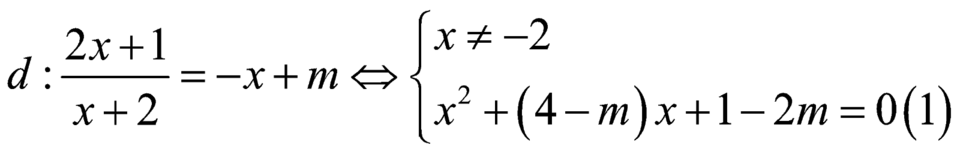  

Gọi . Ta tính được khi m = 0

Xét phương trình hoành độ giao điểm của (d) và (P):

x 2 = m x + 5 ⇔ x 2 − m x − 5 = 0 .

Ta có tích hệ số  a c = − 5 < 0  nên phương trình hoành độ giao điểm luôn có 2 nghiệm phân biệt với mọi m hay thẳng (d) cắt parabol (P) tại hai điểm phân biệt với mọi m.

Theo hệ thức Vi-ét ta có x 1 + x 2 = m x 1 x 2 = − 5 Ta có:

x 1 > x 2 ⇔ x 1 2 > x 2 2 ⇔ x 1 2 − x 2 2 > 0 ⇒ x 1 + x 2 x 1 − x 2 > 0

Theo giả thiết:  x 1 < x 2 ⇔ x 1 − x 2 < 0  do đó  x 1 + x 2 < 0 ⇔ m < 0 .

Vậy thỏa mãn yêu cầu bài toán.

a: Phương trình hoành độ giao điểm là: \(x^2-mx+m-1=0\)

\(\Delta=\left(-m\right)^2-4\cdot\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2\)

Để (P) cắt (d) tại hai điểm phân biệt thì m-2<>0

hay m<>2

b: \(\left|x_A-x_B\right|< 3\)

\(\Leftrightarrow\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}< 3\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2< 9\)

\(\Leftrightarrow m^2-4\left(m-1\right)< 9\)

\(\Leftrightarrow\left(m-2\right)^2-3< 0\)

=>(m+1)(m-5)<0

=>-1<m<5

Phương trình hoành độ giao điểm là:

\(x^2-mx+2m-4=0\)

\(\Delta=\left(-m\right)^2-4\left(2m-4\right)\)

\(=m^2-8m+16=\left(m-4\right)^2\)

Để (P) cắt (d) tại hai điểm phân biệt thì m-4<>0

hay m<>4

Ta có: \(x_1^2+x_2^2\)

\(=\left(x_1+x_2\right)^2-2x_1x_2\)

\(=m^2-2\left(2m-4\right)\)

\(=m^2-4m+8\)

\(=\left(m-2\right)^2+4\ge4\forall x\)

Dấu '=' xảy ra khi m=2

a: PTHĐGĐ là:

x^2+mx-m-2=0(1)

Khi m=2 thì (1) sẽ là

x^2+2x-2-2=0

=>x^2+2x-4=0

=>\(\left[{}\begin{matrix}x=-1+\sqrt{5}\\x=-1-\sqrt{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=6-2\sqrt{5}\\y=6+2\sqrt{5}\end{matrix}\right.\)

b: Δ=m^2-4(-m-2)

=m^2+4m+8

=(m+2)^2+4>0 với mọi x

=>(d) luôn cắt (P) tại hai điểm phân biệtx

x1^2+x2^2=7

=>(x1+x2)^2-2x1x2=7

=>(-m)^2-2(-m-2)=7

=>m^2+2m+4-7=0

=>m^2+2m-3=0

=>m=-3 hoặc m=1