Cho đường tròn tâm O và điểm M nằm ngoài đường tròn.Từ M kẻ hai tiếp tuyến MA và MB ( A,B là các tiếp điểm ). Đường thẳng BO cắt đường tròn tại điểm thứ hai là C, đường thẳng MC cắt đường tròn tại điểm thứ hai là E, đường thẳng AE cắt OM tại F, H là giao điểm của MO và AB
Chứng minh rằng: a) Tứ giác MAOB nội tiếp
b) △ MHE ∼ △ MCD
c) HF = MF
❤ɜ❤ ❤ɜ❤ ❤ɜ❤



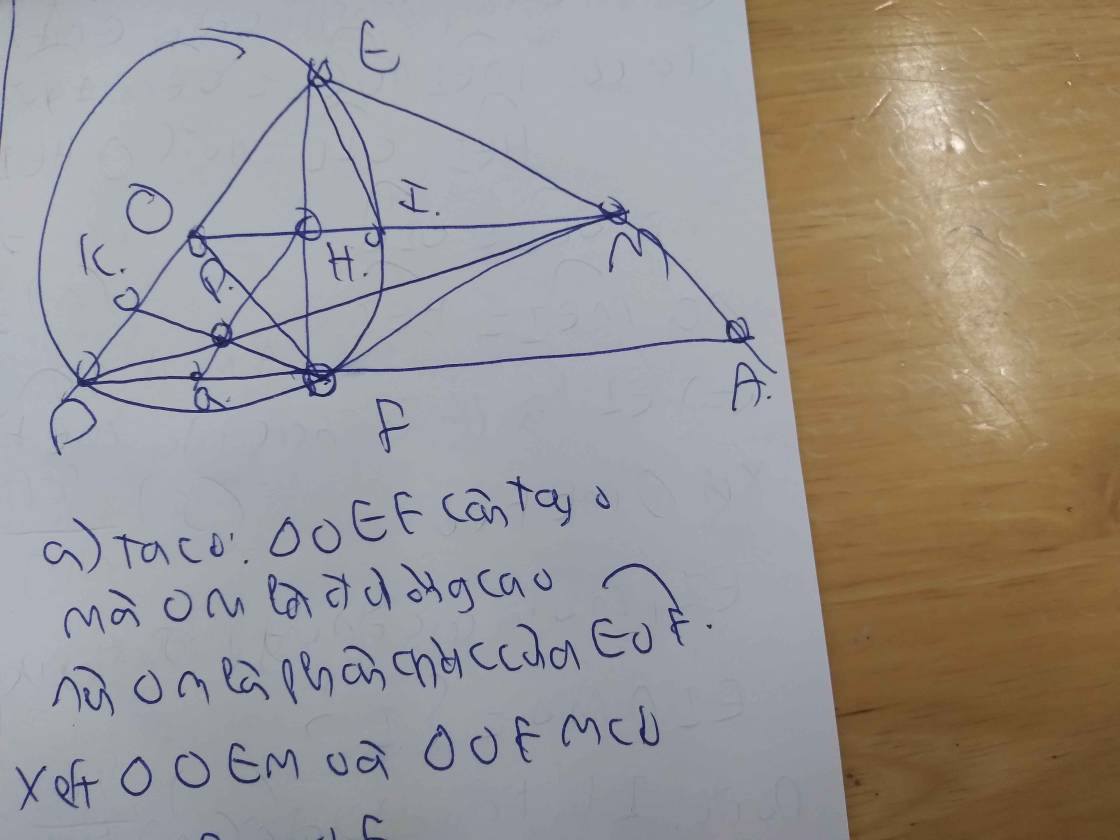







a) Xét tứ giác MAOB có:
\(\widehat{MAO}=90^0\) (MA là tiếp tuyến)
\(\widehat{MBO}=90^0\)(MB là tiếp tuyến)
⇒ \(\widehat{MAO}+\widehat{MBO}=180^0\)
mà hai góc nằm ở vị trí đối nhau
⇒ Tứ giác MAOB nội tiếp (dhnb)
mình giải thế này thôi nha còn lại bạn xem lại đề bài hình như bị sai