A.

$a^2+4b^2+9c^2=2ab+6bc+3ac$

$\Leftrightarrow a^2+4b^2+9c^2-2ab-6bc-3ac=0$

$\Leftrightarrow 2a^2+8b^2+18c^2-4ab-12bc-6ac=0$

$\Leftrightarrow (a^2+4b^2-4ab)+(a^2+9c^2-6ac)+(4b^2+9c^2-12bc)=0$

$\Leftrightarrow (a-2b)^2+(a-3c)^2+(2b-3c)^2=0$

$\Rightarrow a-2b=a-3c=2b-3c=0$

$\Rightarrow A=(0+1)^{2022}+(0-1)^{2023}+(0+1)^{2024}=1+(-1)+1=1$

B.

$x^2+2xy+6x+6y+2y^2+8=0$

$\Leftrightarrow (x^2+2xy+y^2)+y^2+6x+6y+8=0$

$\Leftrightarrow (x+y)^2+6(x+y)+9+y^2-1=0$

$\Leftrightarrow (x+y+3)^2=1-y^2\leq 1$ (do $y^2\geq 0$ với mọi $y$)

$\Rightarrow -1\leq x+y+3\leq 1$

$\Rightarrow -4\leq x+y\leq -2$

$\Rightarrow 2020\leq x+y+2024\leq 2022$

$\Rightarrow A_{\min}=2020; A_{\max}=2022$

\(\dfrac{1}{a-2b}.\sqrt{b^2\left(a^2-4ab+4b^2\right)}=\dfrac{1}{a-2b}.b.\left|a-2b\right|=\dfrac{1}{a-2b}.b.\left(2b-a\right)=-b\)

\(\dfrac{1}{a-2b}\cdot\sqrt{b^2\cdot\left(a^2-4ab+b^2\right)}\)

\(=\dfrac{1\cdot\left(a-2b\right)}{a-2b}\cdot b\)

=b

Ta có  a 2 + 4 b 2 = 12 a b ⇔ a + 2 b 2 = 16 a b

Suy ra 

2 log 3 a + 2 b = log 3 2 4 + log 3 a + log 3 b ⇔ log 3 a + 2 b = 2 log 3 2 + 1 2 log 3 a + log 3 b

 Do đó cả hai mệnh đề đều sai

Đáp án C

Đề có gì đó sai sai

1: \(a^2-4b^2-2a-4b\)

\(=\left(a-2b\right)\left(a+2b\right)-2\left(a+2b\right)\)

\(=\left(a+2b\right)\left(a-2b-2\right)\)

2: \(x^3+2x^2-2x-1\)

\(=\left(x-1\right)\left(x^2+x+1\right)+2x\left(x-1\right)\)

\(=\left(x-1\right)\left(x^2+3x+1\right)\)

Lời giải:

$(a+2b-c)(a+2b+c)-(a^2+4b^2-c^2)=(a+2b)^2-c^2-a^2-4b^2+c^2$

$=(a+2b)^2-a^2-4b^2$

$=a^2+4ab+4b^2-a^2-4b^2=4ab$

\(=\left[\left(a+2b\right)^2-c^2\right]-\left(a^2+4b^2-c^2\right)\)

\(=a^2+4ab+4b^2-c^2-a^2-4b^2+c^2\)

\(=4ab\)

Điều kiện x ≥ − 7 y ≥ − 1 3 *

x 2 + 2 x y + 8 x = 3 y 2 + 12 y + 9             ( 1 ) x 2 + 4 y + 18 − 6 x + 7 − 2 x 3 y + 1 = 0       ( 2 )

Có 1 ⇔ x 2 + 2 y + 4 x − 3 y 2 − 12 y − 9   = 0 , ta coi (1) là phương trình bậc hai ẩn x và y là tham số, giải x theo y ta được x = − 3 y − 9 x = y + 1

Với x = − 3 y − 9 thì (*) ⇒ − 3 y − 9 ≥ − 7 y ≥ − 1 3 ⇔ y ≤ − 2 3 y ≥ − 1 3 (vô lí)

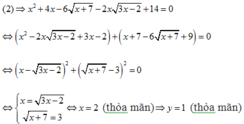
Hệ phương trình có nghiệm là 2 ; 1 ⇒ a = 2 , b = 1 ⇒ T = 24

Đáp án cần chọn là: A