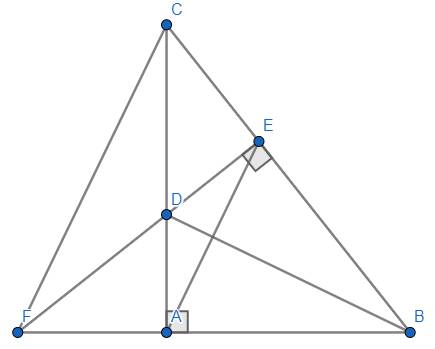
Cho tam giác ABC vuông tại A. Kẻ đường phân giác BD, kẻ DE vuông góc với BC tại E.
a) Chứng minh rằng: BD là trung trực của AE và AD<DC.
b) Tia ED cắt tia BA tại F. Chứng minh BD vuông góc với CF và AE//CF.
c) Tia BD cắt FC tại G. Chứng minh rằng D cách đều ba cạnh của tam giác AEG.
d) Lấy M và N tương ứng di động trên BF và BC sao cho BM+BN=BC. Chứng minh rằng trung điểm I của MN luôn nằm trên một đường thẳng cố định.