CMR : \(2009^{2n}+14\) chia hết cho 5
Câu 2 :
Với 3 mảnh bìa trên đó viết các số 23 , 79 , ab , người ta ghếp chúng thành các số có 6 chữ số khác nhau có thể được . Rồi tính tổng của chúng được 2989896. Tính ab
Câu 3 :
Cho các số tự nhiên từ 1 đến 11 được viết theo thứ tự tùy ý sau đó công mỗi số với thứ tự của nó ta được một tổng . CMR trông tổng nhận được bao giờ cũng tìm được 2 tổng mà hiệu của chúng là một số chia hết cho 10
Câu 4 :
Tìm tất cả các số tự nhiên có 3 chữ số abc để tổng của 6 số có 2 chữ số khác nhau được viết từ các số a,b,c bằng abc


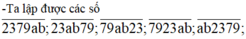

mk làm câu 1:
Ta cso công thức:..9^2n(với n là số nguyên) có tận cùng =1
Ta có:2009^2n+14
=...1+14=...5 chia hết cho 5