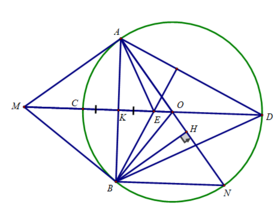
Cho đường tròn 0 và một điểm P ở ngoài đường tròn. Kẻ 2 tiếp tuyến PA, PB với đường tròn O( A,B là tiếp điểm) PO cắt đường tròn tại K và I ( K nằm giữa P và (O) và cắt AB tại H. Gọi D là điểm đối xứng của B qua O, C là giao điểm của PD và đường tròn (O).
a, C/m tứ giác BHCP nội tiếp
b, C/m AC vuông góc CH
c, Đường tròn ngoại tiếp tam giác ACH cắt IC tại M. Tia AM cắt IB tại Q. C/m M là trung điểm AQ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Theo tính chất hai tiếp tuyến cắt nhau ta có ngay \(\widehat{PHB}=90^o\)
Lại có D đối xứng với B qua O nên BD là đường kính đường tròn (O)
Vậy thì \(\widehat{BCD}=90^o\Rightarrow\widehat{PCB}=90^o\)
Xét tứ giác BHCP có \(\widehat{PCB}=\widehat{PHB}=90^o\) mà C và H là hai đỉnh kề nhau nên BHCP là tứ giác nội tiếp.
b) Do BHCP là tứ giác nội tiếp nên \(\widehat{HCD}=\widehat{PBH}\) (Góc ngoài tại một đỉnh bằng góc trong đỉnh đối diện với nó)
Lại có \(\widehat{ACD}=\widehat{ABD}\) (Hai góc nội tiếp cùng chắn cung AD)
\(\Rightarrow\widehat{ACH}=\widehat{ACD}+\widehat{DCH}=\widehat{ABD}+\widehat{PBH}=\widehat{PBD}=90^o\)
Vậy nên AC vuông góc CH.
c) Tứ giác CHMA nội tiếp nên \(\widehat{CAH}=\widehat{CMH}\) (Hai góc nội tiếp cùng chắn cung CH)
Lại có \(\widehat{CAH}=\widehat{CAB}=\widehat{CIB}\) (Hai góc nội tiếp cùng chắn cung CB)
Vậy nên \(\widehat{CMH}=\widehat{CIB}\)
Chúng lại ở vị trí đồng vị nên HM // Bi
Xét tam giác ABQ có H là trung điểm AB, HM // BI nên HM là đường trung bình tam giác ABQ.
Suy ra M là trung điểm AQ.
a) Theo tính chất hai tiếp tuyến cắt nhau ta có ngay = 90 o Lại có D đối xứng với B qua O nên BD là đường kính đường tròn (O) Vậy thì = 90 o⇒ = 90 o Xét tứ giác BHCP có = = 90 o mà C và H là hai đỉnh kề nhau nên BHCP là tứ giác nội tiếp. b) Do BHCP là tứ giác nội tiếp nên = (Góc ngoài tại một đỉnh bằng góc trong đỉnh đối diện với nó) Lại có = (Hai góc nội tiếp cùng chắn cung AD) ⇒ = + = + = = 90 o Vậy nên AC vuông góc CH. c) Tứ giác CHMA nội tiếp nên = (Hai góc nội tiếp cùng chắn cung CH) Lại có = = (Hai góc nội tiếp cùng chắn cung CB)

d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB

Để chứng minh HM.KN=HN.KM, ta sẽ sử dụng định lí Ptolemy cho tứ giác HMIN và KMNO.
Ta có:
Tứ giác HMIN là tứ giác nội tiếp do hai tiếp tuyến IM và IN của đường tròn (O).
Tứ giác KMNO là tứ giác điều hòa do K là điểm đối xứng của M qua O.
Áp dụng định lí Ptolemy cho tứ giác HMIN, ta được:
HM.IN + HN.IM = HI.MN
Áp dụng định lí Ptolemy cho tứ giác KMNO, ta được:
KM.NO + KO.MN = KN.MO
Vì K là điểm đối xứng của M qua O nên KO=OM. Thay vào biểu thức trên, ta được:
KM.NO + OM.MN = KN.MO
KM.NO + MN² = KN.MO
Nhân cả hai vế của phương trình trên với IM.IN, ta được:
KM.NO.IM.IN + MN².IM.IN = KN.MO.IM.IN
HM.KN + MN².IM.IN = HN.KM.IM.IN
Từ đó suy ra:
HM.KN = HN.KM + MN²/IM.IN
Nhưng IM và IN lần lượt là đường cao của tam giác HIM và tam giác HIN nên:
IM.IN = HM.HN
Thay vào biểu thức trên, ta được:
HM.KN = HN.KM + MN²/HM.HN
Ta thấy rằng tam giác HIM và tam giác HIN đồng dạng nên:
HM/HN = IM/IN
Thay vào biểu thức trên, ta được:
HM.KN = HN.KM + MN².IM²/IN²
Vì tam giác HIM và tam giác HIN đồng dạng nên:
IM/IN = HM/HN
Thay vào biểu thức trên, ta được:
HM.KN = HN.KM + MN².HM²/HN²
Điều này chứng tỏ HM.KN=HN.KM nên ta đã chứng minh được điều phải chứng minh.