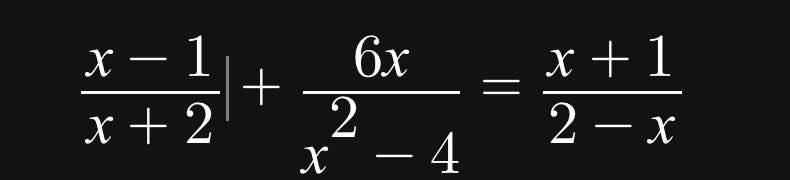A,d của câu nào vậy ah tại mình hỏi đến 4 câu hỏi lận🥲🥲

7:

A+B

\(=x^4-2xy+y^2+y^2+2xy+x^2+1\)

=x^4+2y^2+x^2+1

A-B

=x^4-2xy+y^2-y^2-2xy-x^2-1

=x^4-4xy-x^2-1

5:

a: =8x^2-4x^2=4x^2

b: =(5-7)*x^2y^3z^3=-2x^2y^3z^3

c: =(3+2-1/3-1/2-1/6)*x^2y^2

=4x^2y^2

Câu 2.

Nhiệt lượng bếp tỏa ra trong thời gian \(t=3min=180s\) là:

\(Q=UIt=RI^2t=60\cdot2,5^2\cdot180=675000J\)

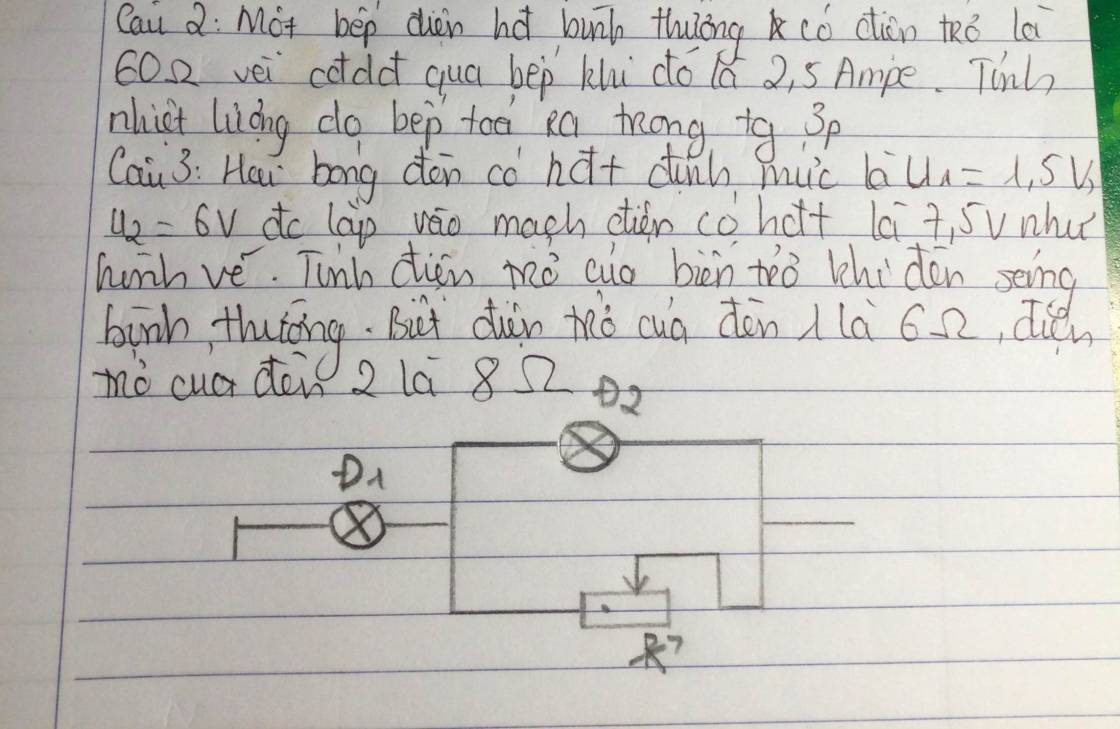
Câu 3.

\(I_{Đ1}=\dfrac{U_{Đ1}}{R_{Đ1}}=\dfrac{6}{6}=1A\)

\(I_{Đ2}=\dfrac{U_{Đ2}}{R_{Đ2}}=\dfrac{1,5}{8}=\dfrac{3}{16}A\)

\(I_b=I_{Đ1}-I_{Đ2}=1-\dfrac{3}{16}=\dfrac{13}{16}A\)

\(R_b=\dfrac{U_b}{I_b}=\dfrac{1,5}{\dfrac{13}{16}}=\dfrac{24}{13}\Omega\)

14: \(=\dfrac{4x+7+1}{\left(x+2\right)\left(4x+7\right)}=\dfrac{4}{4x+7}\)

D

\(lim\dfrac{2\sqrt{7n^2-2n}}{3n+2}=lim\dfrac{2\sqrt{n^2\left(7-\dfrac{2}{n}\right)}}{3n+2}=lim\dfrac{2n\sqrt{7-\dfrac{2}{n}}}{n\left(3+\dfrac{2}{n}\right)}\)

\(=lim\dfrac{2\sqrt{7-\dfrac{2}{n}}}{3+\dfrac{2}{n}}=\dfrac{2\sqrt{7}}{3}\) \(=\dfrac{a\sqrt{7}}{b}\) 

Suy ra : a/b = 2/3 => a - b = -1 

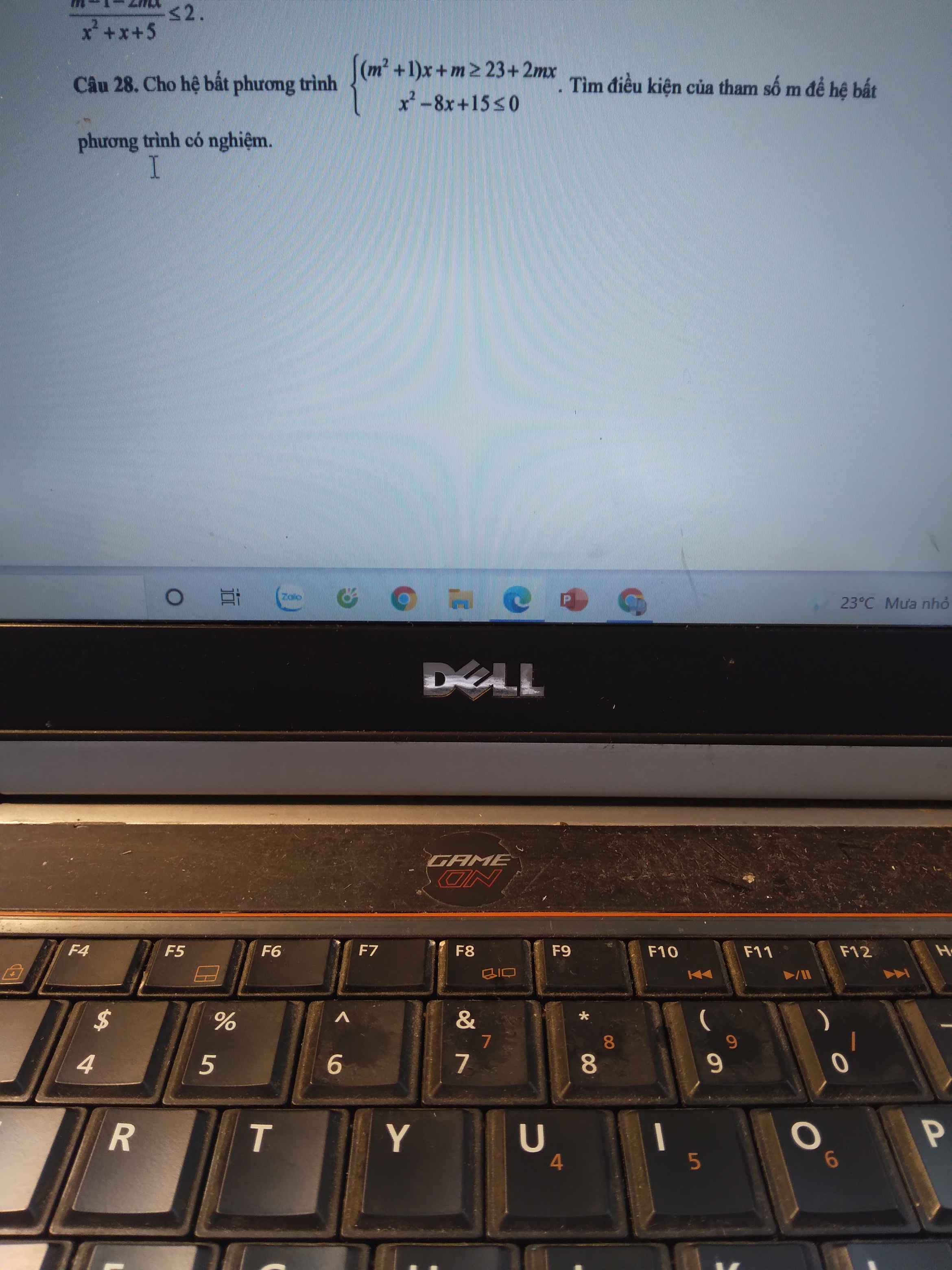
Xét BPT: \(x^2-8x+15\le0\Leftrightarrow3\le x\le5\Rightarrow D_1=\left[3;5\right]\)

Xét BPT: \(\left(m^2+1\right)x+m\ge23+2mx\)

\(\Leftrightarrow\left(m^2-2m+1\right)x\ge23-m\)

\(\Leftrightarrow\left(m-1\right)^2x\ge23-m\) (1)

- Với \(m=1\Rightarrow\left(1\right)\) trở thành \(0\ge22\) (vô lý) \(\Rightarrow\left(1\right)\) vô nghiệm (loại)

- Với \(m\ne1\Rightarrow\left(m-1\right)^2>0;\forall m\)

\(\left(1\right)\Leftrightarrow x\ge\dfrac{23-m}{\left(m-1\right)^2}\) \(\Rightarrow D_2=\left[\dfrac{23-m}{(m-1)^2};+\infty \right)\)

Hệ đã cho có nghiệm khi và chỉ khi \(D_1\cap D_2\ne\varnothing\)

\(\Rightarrow\dfrac{23-m}{\left(m-1\right)^2}\le5\)

\(\Leftrightarrow23-m\le5\left(m-1\right)^2\)

\(\Leftrightarrow5m^2-9m-18\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-\dfrac{6}{5}\end{matrix}\right.\)

\(\dfrac{x-1}{x+2}+\dfrac{6x}{x^2-4}=\dfrac{x+1}{2-x}\left(dkxd:x\ne\pm2\right)\)

\(\Leftrightarrow\dfrac{x-1}{x+2}+\dfrac{6x}{\left(x-2\right)\left(x+2\right)}=-\dfrac{x+1}{x-2}\)

\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)+6x+\left(x+1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=0\)

\(\Leftrightarrow x^2-2x-x+2+6x+x^2+2x+x+2=0\)

\(\Leftrightarrow2x^2+6x+4=0\)

\(\Leftrightarrow2x^2+2x+4x+4=0\)

\(\Leftrightarrow2x\left(x+1\right)+4\left(x+1\right)=0\)

\(\Leftrightarrow\left(2x+4\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+4=0\\x+1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-2\left(ktm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)

Vậy \(S=\left\{-1\right\}\)

  “Lặng lẽ Sa Pa” là chuyện ngắn xoay quanh về nhân vật chính là một anh thanh niên 27 tuổi làm công tác khí tượng thuỷ văn kiêm vật lý địa cầu. Vì vậy anh sống và làm việc một mình trên đỉnh núi Yên Sơn quanh năm mây mù bao phủ. Trong một lần anh gặp gỡ với ông họa sĩ và cô kĩ sư, họ cùng lên thăm chỗ anh ở. Anh giới thiệu với họ về công việc và cuộc sống hàng ngày của mình. Công việc anh đòi hỏi tinh thần trách nghiệm cao nên anh tự tạo cho mình cuộc sống đầy đủ về vật chất và tinh thần. Anh có một căn nhà ngăn nắp, ngọn gàng, có vườn rau, vườn hoa và có sách là bạn. Anh tặng vợ bác lái xe củ tam thất, tặng cô kĩ sư bó hoa, tặng ông họa sĩ một giỏ trứng. Ông họa sĩ già  ngưỡng mộ anh thanh niên nên đã phác họa một bức chân dung nhưng anh đã từ chối. Qua lời kể của anh, các vị khách còn được biết thêm về rất nhiều gương sáng hết lòng phục vụ sự nghiệp xây dựng và chiến đấu bảo vệ Tổ quốc. Sau một lúc nói chuyện họ chia tay. Song anh đã để lại những ấn tượng tốt trong lòng ông họa sĩ và cô kĩ sư, ông họa sĩ đã hứa sẽ có dịp quay trở lại thăm anh.​