5. a) Cho phương trình x - 5x + m = 0 . Tìm m để phương trình có đúng 2 nghiệm phân biệt.
b) Cho a, b là các số dương thỏa mãn ab = 1.
Tìm giá trị nhỏ nhất của biểu thức A = ( a + b + 1 ).( a² + b²) + 4/a+b
(•´︶`•)ฅ♡ yêu nhiều.
6. Cho hai đường tròn (O,R) và (O',R') với R>R' cắt nhau tại A và B. Kẻ tiếp tuyến chung DE của hai đường tròn với D thuộc (O) và E thuộc (O') sao cho B gần tiếp tuyến đó hơn so với A.
a) Chứng minh rằng góc DAB = góc BDE.
b) Tia AB cắt DE tại M. Chứng minh M là trung điểm của DE.
c) Đường thẳng EB cắt DA tại P , đường thẳng DB cắt AE tại Q. Chứng minh rằng PQ // DE.
・゚・(。>д<。)・゚・ xin cảm ơn.


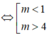
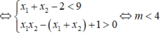
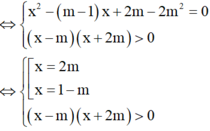
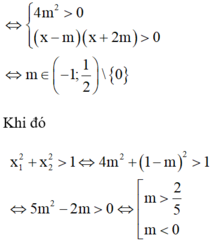


Câu 5:
a/ Để pt có đúng 2 nghiệm pb \(\Leftrightarrow\Delta=25-4m>0\Rightarrow m< \frac{25}{4}\)
b/ \(A=\left(a+b+1\right)\left(a^2+b^2\right)+\frac{4}{a+b}=\left(a+b\right)\left(a^2+b^2\right)+a^2+b^2+\frac{4}{a+b}\)
\(A\ge2\sqrt{ab}.2\sqrt{a^2b^2}+\frac{\left(a+b\right)^2}{2}+\frac{4}{a+b}\)
\(A\ge4+\frac{\left(a+b\right)^2}{4}+\frac{\left(a+b\right)^2}{4}+\frac{2}{a+b}+\frac{2}{a+b}\)
\(A\ge4+\frac{1}{4}.4ab+3\sqrt[3]{\frac{2.2.\left(a+b\right)^2}{4\left(a+b\right)\left(a+b\right)}}=8\)
\(\Rightarrow A_{min}=8\) khi \(a=b=1\)
//Hình học bó tay :(