ai giải giúp mình với mình đang cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài1:Tại vì châm lửa lửa sẽ tác dụng với oxi để cháy
Bài2:vì nó sẽ đẩy nhiều oxi vào bên trong oxi sẽ tác dụng vs lửa và cháy to hơn bạn đầu
Bài3: thổi mạnh vào ngọn nến thì ngọn nến sẽ tắt vì khí mình thổi ra là khí cacbonic
Chúc bạn học tốt

Bài 1:
(x-6)^2020+2(y+3)^2022=0
=>x-6=0 và y+3=0
=>x=6 và y=-3


Bài 2:
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{45}{9}=5\)
Do đó: a=10; b=15;c=20

2: Thay x=1 và y=-4 vào (d), ta được:
2m+2=-4
hay m=-3

Bài 3:
a. \(R=R1+R2=15+30=45\Omega\)
b. \(\left\{{}\begin{matrix}I=U:R=9:45=0,2A\\I=I1=I2=0,2A\left(R1ntR2\right)\end{matrix}\right.\)
c. \(\left\{{}\begin{matrix}U1=R1.I1=15.0,2=3V\\U2=R2.I2=30.0,2=6V\end{matrix}\right.\)
Bài 4:
\(I1=U1:R1=6:3=2A\)
\(\Rightarrow I=I1=I2=2A\left(R1ntR2\right)\)
\(U=R.I=\left(3+15\right).2=36V\)
\(U2=R2.I2=15.2=30V\)

Số học sinh mặc áo xanh chiếm số phần tổng số học sinh tham gia đồng diễn là:
\(1-\frac{2}{5}-\frac{1}{4}=\frac{7}{20}\)(tổng số học sinh)
Đáp số: \(\frac{7}{20}\)
TL:
Gọi tổng số học sinh là: 1
Số học sinh mặc áo xanh chiếm số phần là:
1 - (1/4 + 2/5) = 7/20 (phần số học sinh)
Đáp số: 7/20 phần số học sinh.
HT

Bài 3:
a: Gọi OK là khoảng cách từ O đến AB
Suy ra: K là trung điểm của AB
hay \(AK=BK=\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔOKA vuông tại K, ta được:
\(OA^2=OK^2+KA^2\)
hay OK=3(cm)

\(a, 48.19+81.48\)
\(=49.(19+81)\)
\(=49.100=4900\)
\(b,23.134-34.23\)
\(=23.(134-34)\)
\(=23.100=2300\)

\(x^2-2\left(m-2\right)x+m^2+2m-3=0\left(1\right)\)
Để phương trình có hai nghiệm phân biệt thì Δ' > 0
\(\Rightarrow\left(m-2\right)^2-m^2-2m+3>0\Leftrightarrow m^2-4m+4-m^2-2m+3>0\Leftrightarrow-6m+7>0\Leftrightarrow m< \dfrac{7}{6}\)\)
Theo viét : \(\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-2\right)\\x_1x_2=m^2+2m-3\end{matrix}\right.\)\)
Lại có :\( \dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{5}\)
\(\Leftrightarrow\dfrac{x_1+x_2}{x_1x_2}=\dfrac{x_1+x_2}{5}\)
\(\Rightarrow\left(x_1+x_2\right)\left(x_1x_2\right)=5\left(x_1+x_2\right)\)
\(\Leftrightarrow\left(2m-4\right)\left(m^2+2m-3\right)=5\left(2m-4\right)\)
\(\Leftrightarrow2m^3+4m^2-6m-4m^2-8m+12=10m-20\)
\(\Leftrightarrow2m^3-24m+32=0\) \(\Leftrightarrow\left[{}\begin{matrix}m=-4\left(n\right)\\m=2\left(l\right)\end{matrix}\right.\)
Vậy \(m=-4\) thì thỏa điều kiện







 , mình đang cần giải gấp. Cảm ơn mn nhiều.
, mình đang cần giải gấp. Cảm ơn mn nhiều.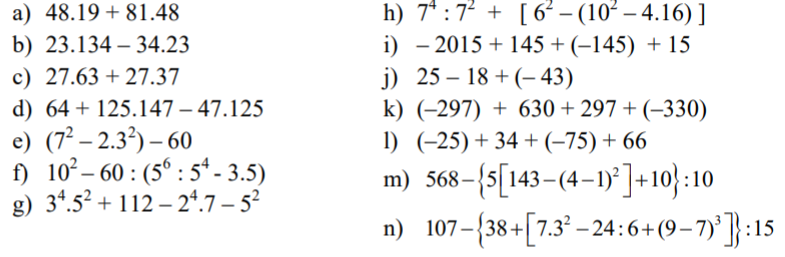

a, 230 + [32 + (x - 5)] =315
32 + (x-5) = 315 - 230
32 + (x-5) =85
x-5=85-32
x-5=53
x=53+5
x=58