Xét tính chẵn lẻ của hàm số: y=ax2 + bx + c, a\(\ne\) 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Nếu \(b=0\) thì hàm chẵn
- Nếu \(b\ne0\) thì hàm không chẵn không lẻ
Đây là hàm bậc 2 nên chỉ có thể là hàm chẵn hoặc hàm ko chẵn ko lẻ.
Khi thay \(x=-x\) thì hệ số a và c ko hề ảnh hưởng nên ko cần xét (do chúng đều là hệ số của hạng tử bậc chẵn)
Nếu đề ko cho \(a\ne0\) thì cần xét trường hợp \(a=0\)

Đặt `y=f(x)=x-sinx`
Có: `f(-x)=-x-sin(-x)=-x+sinx=-(x-sinx)=-f(x)`
`=>` Hàm lẻ.

y = √x
TXĐ: D = [0; +∞) ⇒ x ∈ D thì -x ∉ D
Vậy hàm số trên không là hàm số chẵn cũng không là hàm số lẻ.

Tập xác định D = R và ∀ x ∈ D có -x ∈ D và f(-x) = -2 = f(x)
Hàm số là hàm số chẵn

a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \cot \left( { - x} \right) = - \cot x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \cot x\) là hàm số lẻ.
b)
\(x\) | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\frac{{3\pi }}{4}\) | \(\frac{{5\pi }}{6}\) |
\(\cot x\) | \(\sqrt 3 \) | \(1\) | \(\frac{{\sqrt 3 }}{3}\) | \(0\) | \( - \frac{{\sqrt 3 }}{3}\) | \( - 1\) | \( - \sqrt 3 \) |
c) Từ đồ thị trên, ta thấy hàm số \(y = \cot x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\).


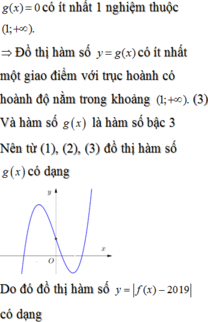
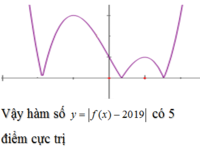

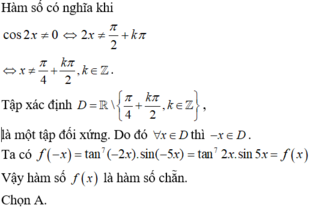

#)Bạn tham khảo nhé :
https://www.nguyentheanh.org/ly-thuyet-va-bai-tap-ve-ham-bac-hai-y-ax2-bx-c-a-%E2%89%A0-0-toan-lop-10/
P/s : Mình k hiểu rõ mấy về toán lớp 10 nhưng được thì bạn cứ tham khảo nhé ^^
Xét tính chẵn lẻ của hàm số: y=ax2 + bx + c
Bạn tham Khảo :
BL