chịu

đọc mà rối loạn tâm chí, chi co cao thủ như các thầy cô giáo mới làm đc

Bài 6 :

Tự vẽ hình nhá :)

a) Gọi O là giao điểm của AC và EF

Xét tam giác ADC có :

EO // DC => AE/AD = AO/AC (1)

Xét tam giác ABC có :

OF // DC

=> CF/CB = CO/CA (2)

Từ (1) và (2) => AE/AD + CF/CB = AO/AC + CO/CA = AO + CO/AC = AC/AC = 1 => đpcm

Bài 7 :

a) Do EF // AB => CF / CA = EF / AB => CF / EF = AC / AB (1)

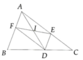
Dựng MG // AC và M là trung điểm của cạnh BC => GM là đường trung bình của tam giác ABC => G là trung điểm của cạnh AB =>AG = BG

Do DK // GM => AD / AG = DK / GM => AD / BG = DK / GM 

=> DK / AD = GM / BG = \(\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB} \left(2\right)\)

Từ (1) và (2) => CF / EF = DK / AD

Mà tứ giác ADEF là hình bình hành ( vì EF // AD và DE // AF ) nên AD = È

=> CF = DK ( đpcm )

Bài 8 : 

Ta có : AB = AM + MB = 11 + 8 = 19 ( cm )

Áp dụng hệ quả định lí Ta-lét vào tam giác ABC, ta có :

AM / AB = AN / AC => AM + AB / AB = AN + AC / AC => 19 + 11 / 19 = AN + 38 / 38 => 30/19 = 38 + AN / 38

=> 1140 = 19.AN + 722

=> AN = ( 1140 - 722 ) / 19 = 22 ( cm )

=> NC = 38 - 12 = 26 ( cm )

chắc sang năm mới làm xong mất 

Qua K vẽ đường thẳng // với AB cắt AC tại H.

=> AHKD là hình bình hành => DK = AH (1)

Gọi giao điểm của AK và DH là O. Vì AHKD là HBH => DO = OH

Xét 3 đường thẳng MA, CA, BA đồng quy tại A cắt 2 đường thẳng DH và BC ta được: DO/OH = BM/MC = 1

=> DH // BC (định lí chùm đường thẳng đồng quy đảo)

Xét ∆ ADH và ∆ FEC có: 

AD = EF ( t/c đoạn chắn) ; DH = EC (t/c đoạn chắn) ; ^ADH = ^FEC => ∆ ADH = ∆ FEC (c-g-c)

=> AH = CF (2)

Từ (1) và (2) => CF = DK (đpcm)

GL

Do EF//AB⇒\(\frac{CF}{CA}=\frac{EF}{AB}\)⇒\(\frac{CF}{EF}=\frac{AC}{AB}\)(1)

Dựng MG//AC và MM là trung điểm cạnh BC

⇒GM là đường trung bình ΔABC

=⇒G là trung điểm cạnh AB ⇒AG=BG

Do DK//GM⇒\(\frac{AD}{AG}=\frac{DK}{GM}\)⇒\(\frac{AD}{BG}=\frac{DK}{GM}\)

=> \(\frac{DK}{AD}=\frac{GM}{BG}=\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB}\left(2\right)\)

Từ (1) và (2)\(\Rightarrow\frac{CF}{EF}=\frac{DK}{AD}\)

Mà tứ giác ADEF là hình bình hành (vì EF//AD và DE//AF) nên AD=EF

=> CF=DK (đpcm)
Nguồn: thuynga

Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I

434

AI TICK GIÙM MÌNH MỘT CÁI ĐI MÀ LÀM ƠN ĐÓ!!!!!!!!!!!!!!!!!!!!!!!