a) Sai 

b) Đúng

c) Đúng

Đề bài

1. Trong bảng sau, cột cuối cùng ghi tỉ số phần trăm giữa số trẻ em đi học và tổng số trẻ em đến  tuổi đi học của một xã. Hãy dùng máy tính bỏ túi để tính rồi viết kết quả vào cột đó.

2. Trung bình bóc 1kg lạc vỏ thì thu được 0,65kg lạc hạt, tức là tỉ số phần trăm giữa lạc hạt và lạc vỏ là 65%. Bằng máy tính bỏ túi, hãy tính số lạc hạt thu được khi bóc vỏ lạc rồi viết vào bảng sau (theo mẫu)

3. Với lãi suất tiết kiệm 0,5%/một tháng, cần gửi bao nhiêu đồng để sau một tháng nhận được số tiền lãi là:

a) 20 000 đồng            

b) 40 000 đồng            

c) 60 000 đồng

(Dùng máy tính bỏ túi để tính)

Đáp án

1. Trong bảng sau, cột cuối cùng ghi tỉ số phần trăm giữa số trẻ em đi học và tổng số trẻ em đến  tuổi đi học của một xã. Hãy dùng máy tính bỏ túi để tính rồi viết kết quả vào cột đó.

2. Trung bình bóc 1kg lạc vỏ thì thu được 0,65kg lạc hạt, tức là tỉ số phần trăm giữa lạc hạt và lạc vỏ là 65%. Bằng máy tính bỏ túi, hãy tính số lạc hạt thu được khi bóc vỏ lạc rồi viết vào bảng sau (theo mẫu)

3. Với lãi suất tiết kiệm 0,5%/một tháng, cần gửi bao nhiêu đồng để sau một tháng nhận được số tiền lãi là:

a) 20 000 đồng

b) 40 000 đồng

c) 60 000 đồng

Bài giải

Số tiền cần gửi để cuối tháng nhận được số tiền 20 000 đồng:

20 000 : 0,5 x 100 = 4 000 000 (đồng)

Số tiền cần gửi để cuối tháng nhận được số tiền 40 000 đồng:

40 000 : 0,5 x 100 = 8 000 000 (đồng)

Số tiền cần gửi để cuối tháng nhận được số tiền 60 000 đồng:

60 000 : 0,5 x 100 = 12 000 000 (đồng)

Đáp số: a) 4 000 000 đồng

             b) 8 000 000 đồng

             c) 12 000 000 đồng

t vứt sách lop5 r

Bài 3.9:

a: =-(7+2)=-9

b: =-(8+5)=-13

bài 3.9:

a)(-7) + (-2)=- (7+2)=-9

b)(-8) + (-5) =-(8+5)=-13

Mik chịu thôi, bó tay.com.

1 . 

Ta có AB = BC (gt)

Suy ra  ∆ABC cân

Nên ˆA1=ˆC1A1^=C1^  (1)

Lại có ˆA1=ˆA2A1^=A2^ (2) (vì AC là tia phân giác của ˆAA^)

Từ (1) và (2) suy ra ˆC1=ˆA2C1^=A2^

nên BC // AD (do ˆC1,ˆA2C1^,A2^ ở vị trí so le trong)

Vậy ABCD là hình thang

Bạn ghi đề mới biết chứ

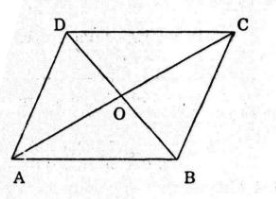
+ ΔAHB và ΔCKD có

      HB = KD (=1)

      góc AHB = góc CKD(=90º)

      AH = CK (=3).

⇒ ΔAHB = ΔCKD(c.g.c)

⇒AB = CD (hai cạnh tương ứng)

+ ΔCEB và ΔAFD có

      BE = DF (=2)

      góc BEC = góc DFA (=90º)

      CE = AF (=4).

⇒ ΔCEB = ΔAFD ( c.g.c)

⇒ BC = AD (hai cạnh tương ứng)

b) ΔABD và ΔCDB có

      AB = CD

      AD = BC

      BD cạnh chung

⇒ ΔABD = ΔCDB (c.c.c)

⇒ góc ABD = góc CDB (hai góc tương ứng)

Vậy AB // CD ( hai gó so le trong bằng nhau )

k minh nha

(hình hơi xấu, thông cảm nha)

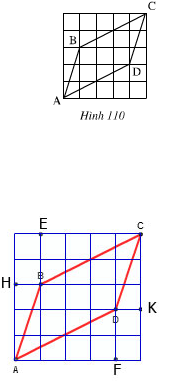
a) Xét \(\Delta AEB\)và \(\Delta DFC\) có: 

AE = DF

\(\widehat{AEB}=\widehat{DFC}=90^o\)

BE = CF

Do đó: \(\Delta AEB=\Delta DFC\) (c.g.c)

Suy ra: AB = DC (đpcm)

Xét \(\Delta BMC\) và \(\Delta DNA\) có:

MC = NA

\(\widehat{BMC}=\widehat{DNA}=90^o\)

BM = DN

Do đó: \(\Delta BMC=\Delta DNA\)

Suy ra: BC = AD (đpcm)

b) Xét \(\Delta ABD\) và \(\Delta CDB\) có:

AB = CD (câu a)

BC = AD (câu a)

BD là cạnh chung

Do đó: \(\Delta ABD=\Delta CDB\) (c.c.c)

Suy ra: \(\widehat{ABD}=\widehat{CDB}\) (so le trong)

=> AB // CD (đpcm)

Phải chép ra người ta mới biết mà giải

sgk toán 8 tập 1

Bài 74. Hai đường chéo của một hình thoi bằng 8cm8cm và 10cm10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:

(A) 6cm6cm;                     (B) √41cm41cm                  

(C) √164cm164cm               (D) 9cm9cm ?

Bài giải:      

Xét bài toán tổng quát:

ABCDABCD là hình thoi, OO là giao điểm hai đường chéo.

Theo tính của hình thoi hai đường chéo của hình thoi vuông góc và cắt nhau tại trung điểm mỗi đường.

Áp dụng định lí Pytago vào tam giác vuông ABOABO ta có:

AB2=OA2+OB2=(12AC)2+(12BD)2⇒AB=√(12AC)2+(12BD)2=√42+52=√41cmAB2=OA2+OB2=(12AC)2+(12BD)2⇒AB=(12AC)2+(12BD)2=42+52=41cm

Vậy (B) đúng.

Bài 79.

a) Một hình vuông có cạnh bằng 3cm3cm. Đường chéo của hình vuông đó bằng 6cm6cm,  √18cm18cm, 5cm5cm hay 4cm4cm ?

b) Đường  chéo của một hình vuông bằng 2dm2dm. Cạnh cảu hình vuông đó bằng: 1dm1dm,

32dm32dm, √2dm2dm hay 43dm43dm ?

Bài giải:

a) Gọi đường chéo của hình vuông có độ dài là aa.

Ta có: a2=32+32=18a2=32+32=18

Suy ra a=√18a=18

Vậy đường chéo của hình vuông đó bằng √18cm18cm.

b) Gọi cạnh của hình vuông là aa.

Ta có  a2+a2=22⇒2a2=4⇒a2=2⇒a=√2a2+a2=22⇒2a2=4⇒a2=2⇒a=2

Vậy cạnh của hình vuông đó bằng √2dm2dm.

nhưng mình hỏi ở sách NÂNG CAO VÀ PHÁT TRIỂN TOÁN 8