Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
c,Vẽ tam giác đều AMD ( D thuộc nửa mặt phẳng bờ AM không chứa C)(Bạn tự vẽ hình nha, dễ như ăn kẹo ấy)
=> DM = AD = AM
Sau đó bạn chứng minh tam giác ADB = tam giác AMC (c.g.c) (cũng dễ thôi)
=> BD = MC (cặp cạnh tương ứng)
Ta có: DM = AM, BD = MC
=> DM : BM : BD = 3:4:5
=> tam giác BDM vuông tại M
=> góc AMB = 90o + 60o = 150o
Em tham khảo link này nhé!
Câu hỏi của channel Anhthư - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo nhé!
Câu hỏi của channel Anhthư - Toán lớp 7 - Học toán với OnlineMath
bạn chơi bang bang ak mà chụp hình ảnh kiếm thần nên có nick bang bang cho mình một nick nhé mình giải bài này cho
Câu hỏi của channel Anhthư - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo nhé!
AMB bằng 150 độ cách làm vẽ thêm tam giác đều MBK ra phía ngoài
c,Vẽ tam giác đều AMD ( D thuộc nửa mặt phẳng bờ AM không chứa C)(Bạn tự vẽ hình nha, dễ như ăn kẹo ấy)
=> DM = AD = AM
Sau đó bạn chứng minh \(\Delta\)ADB = \(\Delta\)AMC (c.g.c) (cũng dễ thôi)
=> BD = MC (cặp cạnh tương ứng)
Ta có: DM = AM, BD = MC
=> DM : BM : BD = 3:4:5
=> \(\Delta\)BDM vuông tại M
=> góc AMB = 90o + 60o = 150o
a, Xét tam giác ABM và AMC có
BC=BA ( tam giác đều )
BMC=BMA=90độ
Góc C=A
=> ABM=AMC
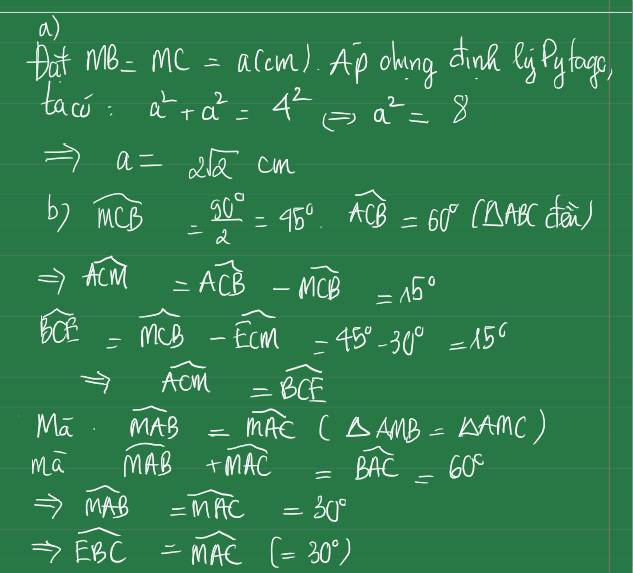
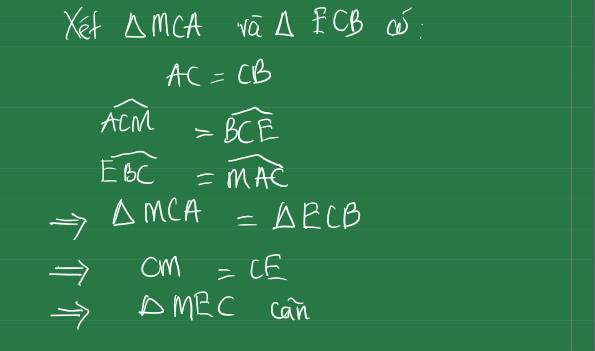
a) Xét tam giác: AMB và AMC có:
AM chung
BM=CM ( gt)
AB=AC ( tam giác ABC đều)
=> Tam giác AMB =Tam giác AMC (1)
b) Xét tam giác MBC vuông cân tại M
=> \(\widehat{MCB}=\frac{90^o}{2}=45^o\)
Tam giác ABC đều
=> \(\widehat{ACB}=60^o\)
=> \(\widehat{ACM}=\widehat{ACB}-\widehat{MCB}=60^o-45^o=15^o\)
\(\widehat{BCE}=\widehat{MCB}-\widehat{ECM}=45^o-30^o=15^o\)
=> \(\widehat{ACM}=\widehat{BCE}\)(2)
Từ (1) => \(\widehat{MAB}=\widehat{MAC}\) mà \(\widehat{MAB}+\widehat{MAC}=\widehat{BAC}=60^o\)
=> \(\widehat{MAB}=\widehat{MAC}=60^o:2=30^o\)
=> \(\widehat{EBC}=\widehat{MAC}\left(=30^o\right)\)(3)
Xét tam giác MCA và tam giác ECB
có: AC=CB ( tam giác ABC đều)
\(\widehat{ACM}=\widehat{BCE}\)( theo (2))
\(\widehat{EBC}=\widehat{MAC}\)( theo (3))
=> Tam giác MCA =Tam giác ECB
=> CM=CE
=> tam giác MEC cân
Câu c) Trên nửa mặt phẳng bờ AM không chứa điểm C dựng tam giác đều AMN
=> \(\widehat{AMN}=60^o\)
và NA=NM=AM
Ta có: \(\widehat{NAB}+\widehat{BAM}=\widehat{NAM}=60^o=\widehat{BAC}=\widehat{BAM}+\widehat{MAC}\)
=> \(\widehat{NAB}=\widehat{MAC}\)(1)
Xét tam giác NAB và tam giác MAC
có: AB=AC ( tam giác ABC đều)
NA=AM ( tam giác AMN đều)
\(\widehat{NAB}=\widehat{MAC}\)( theo (1))
=> Tam giác NAB=MAC
=> NB=MC
Suy ra: MN:BM:NB=MA:MB:MC=3:4:5
=> Tam giác NMB vuông tại M
=> \(\widehat{NMB}=90^o\)
=> \(\widehat{AMB}=\widehat{AMN}+\widehat{NMB}=60^o+90^o=150^o\)