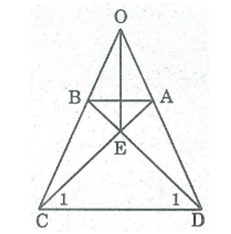
1) hình thang cân ABCD có O là giao điểm của hai đường thẳng chứa cạnh bên AD,BC và E là giao điểm của hai đường chéo. Chứng minh OE là đường trung trực hai đáy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 7 2019
Vì ABCD là hình thang cân
Gọi H là giao điểm AB và OE
=> AB // CD
ADC = BCD
Mà OAB = ADC ( đồng vị)
BCD = OBA ( đồng vị)
Mà ADC = BCD
=> ∆BOA cân tại O
Tự xét ∆OAH = ∆OBH(c.g.c)
=> HA = HB
=> OH vuông góc với AB
Hay OE vuông góc với AB
=> OE là trung trực AB
Gọi G là giao điểm DC và OE
Mà AB//CD(cmt)
=> GHB = HGD = 90°
=> OG vuông góc với DC
Hay OE vuông góc với DC
Tự xét ∆ACD = ∆BDC
=> DAE = CBE ( tg ứng )
Tự xét ∆AED = ∆BEC (g.c.g)
=> DE = EC
=> DEC cân tại E
Mà ∆DEC có OH là đường cao
=> OH là trung trực DC
Hay OE là trung trực DC(dpcm)
23 tháng 9 2020
Vì ABCD là hình thang cân
Gọi H là giao điểm AB và OE
=> AB // CD
ADC = BCD
Mà OAB = ADC ( đồng vị)
BCD = OBA ( đồng vị)
Mà ADC = BCD
=> ∆BOA cân tại O
Tự xét ∆OAH = ∆OBH(c.g.c)
=> HA = HB
=> OH vuông góc với AB
Hay OE vuông góc với AB
=> OE là trung trực AB
Gọi G là giao điểm DC và OE
Mà AB//CD(cmt)
=> GHB = HGD = 90°
=> OG vuông góc với DC
Hay OE vuông góc với DC
Tự xét ∆ACD = ∆BDC
=> DAE = CBE ( tg ứng )
Tự xét ∆AED = ∆BEC (g.c.g)
=> DE = EC
=> DEC cân tại E
Mà ∆DEC có OH là đường cao
=> OH là trung trực DC
Hay OE là trung trực DC
28 tháng 8 2016
1.
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB
11 tháng 8 2020
Ta có: ∠(ADC) = ∠(BCD) (gt)
⇒ ∠(ODC) = ∠(OCD)
⇒ΔOCD cân tại O (dhnb tam giác cân)
⇒ OC = OD
OB + BC = OA + AD
Mà AD = BC (hình thang ABCD cân)
⇒ OA = OB
Xét ΔADC và. ΔBCD:
AD = BC (hình thang ABCD cân )
AC = BD (hình thang ABCD cân)
CD chung
Do đó ΔADC và ΔBCD (c.c.c)
⇒ ∠D1= ∠C1
⇒ΔEDC cân tại E (dhnb tam giác cân)
⇒ EC = ED nên E thuộc đường trung trực CD
OC = OD nên O thuộc đường trung trực CD
E ≠ O. Vậy OE là đường trung trực của CD.
Ta có: BD= AC (hình thang ABCD cân)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
Mà OA = OB (cmt)
Nên O thuộc đường trung trực của AB
E ≠ O. Vậy OE là đường trung trực của AB.
CM
8 tháng 2 2017
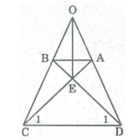
Ta có: ∠ (ADC) = ∠ (BCD) (gt)
⇒ ∠ (ODC) = ∠ (OCD)
⇒ ∆ OCD cân tại O
⇒ OC = OD
OB + BC = OA + AD
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ∆ ADC và ∆ BCD:
AD = BC (tính chất hình thang cân )
AC = BD (tính chất hình thang cân)
CD chung
Do đó ∆ ADC và ∆ BCD (c.c.c)
⇒ ∠ D 1 = ∠ C 1
⇒ ∆ EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực CD
OC = OD nên O thuộc đường trung trực CD
E ≠ O. Vậy OE là đường trung trực của CD.
Ta có: BD= AC (tính chất hình thang cân)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
OA = OB (chứng minh trên ) nên O thuộc đường trung trực của AB
E ≠ O. Vậy OE là đường trung trực của AB.