Câu này khó quá mình làm không ra. Giúp mình với. Mình cảm mơn nhìu nhìu lắm 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=\(\sqrt{2\left(12-6\sqrt{3}\right)}-\sqrt{2\left(28+10\sqrt{3}\right)}\)
=\(\sqrt{2\left(3-\sqrt{3}\right)2}-\sqrt{2\left(5+\sqrt{3}\right)^2}\)
=\(\sqrt{2}\left(3-\sqrt{3}\right)-\sqrt{2}\left(5+\sqrt{3}\right)=\sqrt{2}\left(3-\sqrt{3}-5-\sqrt{3}\right)\)
=\(\sqrt{2}\left(-2-2\sqrt{3}\right)\)=\(-2\sqrt{2}-2\sqrt{6}\)

3:
\(6a+11b-6\left(a+7b\right)\)
\(=6a+11b-6a-42b=-31b⋮31\)
Ta có: \(\left(6a+11b\right)-6\left(a+7b\right)⋮31\)
\(6a+11b⋮31\)
Do đó: \(6\left(a+7b\right)⋮31\)
=>\(a+7b⋮31\)
Ta có: \(\left(6a+11b\right)-6\left(a+7b\right)⋮31\)
\(a+7b⋮31\)
Do đó: \(6a+11b⋮31\)
4:
\(5a+2b⋮17\)
=>\(12\left(5a+2b\right)⋮17\)
=>\(60a+24b⋮17\)
=>\(51a+17b+9a+7b⋮17\)
=>\(17\left(3a+b\right)+\left(9a+7b\right)⋮17\)
mà \(17\left(3a+b\right)⋮17\)
nên \(9a+7b⋮17\)

Ta có: ( x - 2) x ( y + 3) = -13 = (-13) x 1 = (-1) x 13
* Nếu x - 2 = -13 => x = (-13) + 2 = -11
y + 3 = 1 => y = 1-3 = -2
* Nếu x-2 = -1 => x = (-1) + 2 = 1
y + 3 = 13 => y = 13 - 3 = 10
Vậy có 2 cặp x;y x;y(-11;-2)
x;y(1;10)

Có: \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\)
\(\Leftrightarrow\)\(\frac{x^2}{4}=\frac{y^2}{9}=\frac{z^2}{16}\)
Áp dụng tc của dãy tỉ số bằng nhau ta có:
\(\frac{x^2}{4}=\frac{y^2}{9}=\frac{z^2}{16}=\frac{x^2-y^2+2z^2}{4-9+2\cdot16}=\frac{108}{27}=4\)
\(\Rightarrow\begin{cases}x=4;x=-4\\y=6;y=-6\\z=8;z=-8\end{cases}\)
Vậy pt có nghiệm là \(\left[\begin{array}{nghiempt}x=4;y=6;z=8\\x=-4;y=-6;z=-8\end{array}\right.\)

\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\\ \Rightarrow x^3=\left(\sqrt[3]{9+4\sqrt{5}}\right)^3+\left(\sqrt[3]{9-4\sqrt{5}}\right)^3+3\sqrt[3]{9+4\sqrt{5}}\sqrt[3]{9-4\sqrt{5}}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\)
\(\Rightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3.x\\ \Rightarrow x^3=18+3x\)
\(y=\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
\(y^3=\left(\sqrt[3]{3+2\sqrt{2}}\right)^3+\left(\sqrt[3]{3-2\sqrt{2}}\right)^3+3\sqrt[3]{3+2\sqrt{2}}\sqrt[3]{3-2\sqrt{2}}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\)
\(\Rightarrow y^3=3+2\sqrt{2}+3-2\sqrt{2}+3y\)
\(\Rightarrow y^3=6+3y\)
\(P=x^3+y^3-3\left(x+y\right)+1993\)
\(P=18+3x+6+3y-3\left(x+y\right)+1993\)
\(P=2017+3\left(x+y\right)-3\left(x+y\right)\)
\(P=2017\)

\(=\sqrt{\left(2\sqrt{3}+3\right)^2}-\sqrt{\left(2\sqrt{3}-3\right)^2}\)
\(=\left|2\sqrt{3}+3\right|-\left|2\sqrt{3}-3\right|\)
\(=2\sqrt{3}+3-2\sqrt{3}+3\)
\(=6\)

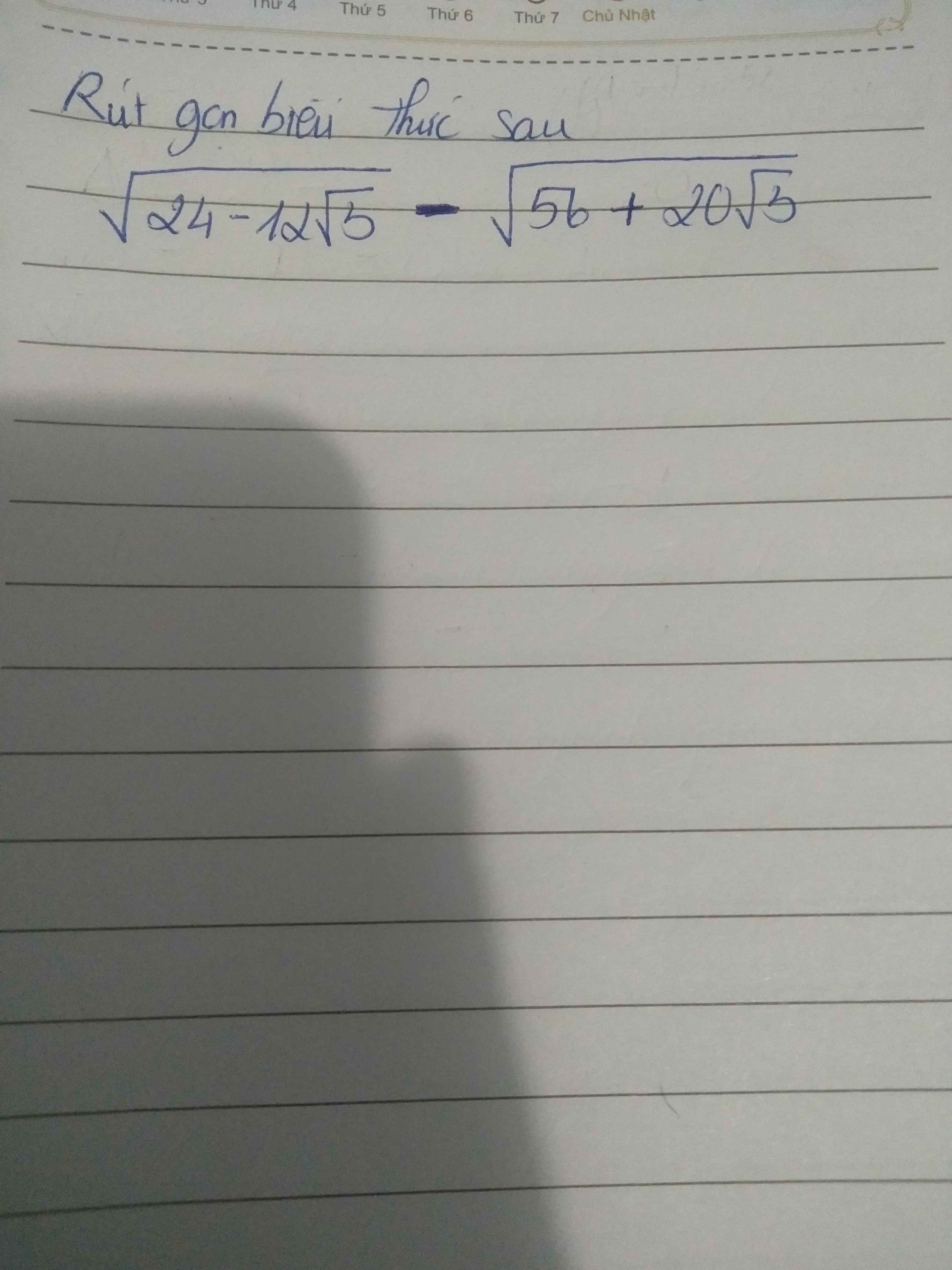



 giúp mình mấy câu này với mình cảm ơn nhìu ạ
giúp mình mấy câu này với mình cảm ơn nhìu ạ
\(\left(\sqrt{5-2\sqrt{6}}+\sqrt{2}\right)\cdot\dfrac{1}{\sqrt{3}}\)
\(=\sqrt{3}\cdot\dfrac{1}{\sqrt{3}}\)
=1
Cho mình hỏi là sao ra được √3 vậy? Tại mình học yếu á. Nên mình không hiểu lắm.