Tìm các giá trị của x để biểu thức sau có giá trị nguyên:
F=x^2-1/x^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài 1:
\(\left(\frac{1}{2}-2\right).\left(\frac{1}{3}-x\right)>0\)
\(\Leftrightarrow\left(-\frac{3}{2}\right)\left(\frac{1}{3}-x\right)>0\)
Để biểu thức \(\left(\frac{1}{2}-2\right)\left(\frac{1}{3}-x\right)\) nhận giá trị dương thì \(-\frac{3}{2}\)và \(\frac{1}{3}-x\)phải cùng âm
\(\Leftrightarrow\frac{1}{3}-x< 0\)
\(\Leftrightarrow x>\frac{1}{3}\)
Vậy \(x>\frac{1}{3}\)thì biểu thức\(\left(\frac{1}{2}-2\right)\left(\frac{1}{3}-x\right)\) nhận giá trị dương
bài 2:
a)Để \(\frac{x^2-2}{5x}\) nhận giá trị âm thì x2-2<0 hoặc 5x<0
+)Nếu x2-2<0
=>x2<2
=>x<\(\sqrt{2}\)
+)Nếu 5x<0
=>x<0
Vậy x<\(\sqrt{2}\)hoặc x<0 thì biểu thức \(\frac{x^2-2}{5x}\)nhận giá trị âm
b)Để E nhận giá trị âm thì \(\frac{x-2}{x-6}\)nhận giá trị âm
=>x-2<0 hoặc x-6<0
+)Nếu x-2<0
=>x<2
+)Nếu x-6<0
=>x<6
Vậy x<2 hoặc x<6 thì biểu thức E nhận giá trị âm

\(F=\frac{x^2-1}{x^2}=1-\frac{1}{x^2}\)
Để \(F< 0\)thì \(1-\frac{1}{x^2}< 0\Leftrightarrow\frac{1}{x^2}>1\Leftrightarrow1>x^2\Leftrightarrow x^2-1< 0\)
\(\Leftrightarrow\left(x+1\right)\left(x-1\right)< 0\Leftrightarrow\hept{\begin{cases}x+1>0\\x-1< 0\end{cases}}\Leftrightarrow-1< x< 1\)và \(x\ne0\)
\(F=\frac{x^2-1}{x^2}\)
Để F đạt giá trị âm
\(\Rightarrow\hept{\begin{cases}x^2-1< 0\\x^2\ne0\end{cases}\Rightarrow\hept{\begin{cases}x^2< 1\\x^2\ne0\end{cases}}\Rightarrow\hept{\begin{cases}x< 1\\x\ne0\end{cases}\Rightarrow}\hept{\begin{cases}-1< x< 1\\x\ne0\end{cases}}}\)
Vậy \(-1< x< 1;x\ne0\) thì C đạt giá trị âm

a, F(\(x\)) = (-2 + \(\dfrac{2}{5}\)\(x\) + 1).(\(x\) - 2024)
-2 + \(\dfrac{2}{5}\)\(x\) + 1 = 0 ⇒ \(\dfrac{2}{5}\)\(x\) = 1 ⇒ \(x\) = \(\dfrac{5}{2}\);
\(x\) - \(2024\) = 0 ⇒ \(x\) = 2024
Lập bảng xét dấu ta có:
| \(x\) | \(\dfrac{5}{2}\) 2024 |
| \(x\) - 2024 | - - 0 + |
| - 2 + \(\dfrac{2}{5}\)\(x\) + 1 | - 0 + + |
| F(\(x\)) | + 0 - 0 + |
Theo bảng trên ta có: F(\(x\)) > 0 ⇔ \(\left[{}\begin{matrix}\dfrac{5}{2}>x\\2024< x\end{matrix}\right.\)
b,F(\(x\) ) = \(\dfrac{x-2}{x+5}\)
\(x\) - 2 = 0 ⇒ \(x\) = 2; \(x\) + 5 = 0 ⇒ \(x\) = -5
Lập bảng xét dấu ta có:
| \(x\) | -5 2 |
| \(x-2\) | - - 0 + |
| \(x+5\) | - 0 + 0 + |
| F(\(x\)) | + 0 - 0 + |
Theo bảng trên ta có: F(\(x\)) > 0 ⇔ \(\left[{}\begin{matrix}x< -5\\x>2\end{matrix}\right.\)

Điều kiện: 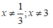
Để biểu thức đã cho có giá trị bằng 2 thì:
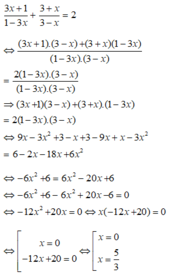
Kết hợp điều kiện phương trình đã cho có 2 nghiệm là x = 0 và x = 5 3
Chọn đáp án A

Điều kiện:
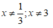
Để biểu thức đã cho có giá trị bằng 2 thì:
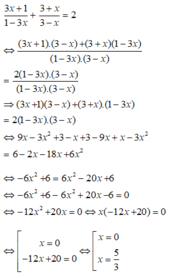
Kết hợp điều kiện phương trình đã cho có 2 nghiệm là x = 0 và x = 5 3
Chọn đáp án A

Bài 1:
a: \(x^2+5x=x\left(x+5\right)\)
Để biểu thức này âm thì \(x\left(x+5\right)< 0\)
hay -5<x<0
b: \(3\left(2x+3\right)\left(3x-5\right)< 0\)
\(\Leftrightarrow-\dfrac{3}{2}< x< \dfrac{5}{3}\)

a.\(16-x^2=0\)
\(\Leftrightarrow x^2=16\)
\(\Leftrightarrow x^2=4^2\)
\(\Leftrightarrow x=\pm4\)
b.\(\left(x+1\right)^2+\left(2y-3\right)^{10}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x+1\right)^2=0\\\left(2y-3\right)^{10}=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\2y-3=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{2}\end{matrix}\right.\)
\(F=\frac{x^2-1}{x^2}=1-\frac{1}{x^2}\)
Để F có gái trị nguyên thì \(1⋮x^2=>x^2=1=>x=\pm1\)