các cặp góc đối đỉnh là \(\widehat{xOy}và\widehat{x'Oy'}\) ;\(\widehat{x'Oy}=\widehat{xOy'}\)

ta có  \(\widehat{xOy}và\widehat{x'Oy'}\) là 2 góc đối đỉnh \(\Rightarrow\text{ }\text{ }\widehat{xOy}=\widehat{x'Oy'}=45độ\)

ta có \(\widehat{x'Oy}+\widehat{xOy}=180độ\)

\(\Rightarrow\widehat{x'Oy}+45độ=180độ\)

\(\Rightarrow\widehat{x'Oy}=180độ-45độ=135độ\)

ta có \(\widehat{x'Oy}=\widehat{xOy'}\) là 2 góc đối đỉnh

\(\Rightarrow\widehat{x'Oy}=\widehat{xOy'}=135độ\)

vậy \(\widehat{x'Oy}=135độ;\widehat{xOy'}=135độ;\widehat{x'Oy'}=45độ\)

Giaỉ:

Ta có: góc zIy = xIt = 45^o (đối đỉnh)

         góc  zIx + xIt = 180^o ( kề bù)

nên zIx + 45^o = 180 ^o

     zIx = 180^o - 45^o

     zIx  = 135^o

=> zIx = 135^o

vậy : yIt  = zIx = 135^o( đối đỉnh)

đáp số:zIy = 45^o

zIx = 135^o

yIt = 135^o

tick nhé hà hoàng

40  độ

mình cũng nghĩ vậy

Ox và Ox' là 2 tia đối nhau

=> xOx' = 180⁰

Oy và Oy' là 2 tia đối nhau

=> yOy' = 180⁰

\(xOx'+3\times yOx'=240^0\)

\(180^0+3\times yOx'=240^0\)

\(3\times yOx'=240^0-180^0\)

\(3\times yOx'=60^0\)

\(yOx'=\frac{60^0}{3}\)

\(yOx'=20^0\)

mà y'Ox = yOx'

=> y'Ox = 20⁰

Mình cảm ơn bạn nhiều nhé 

Ta có :

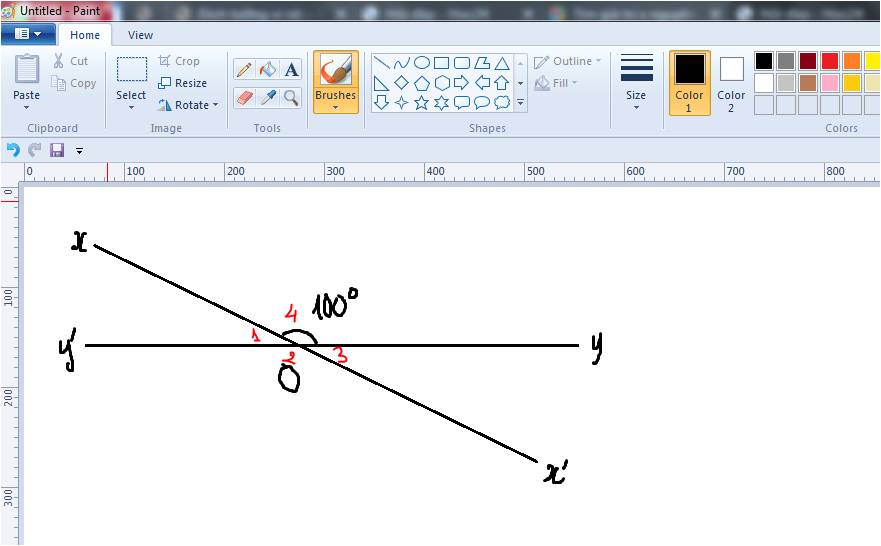
`@)` `\hat{x'Oy'} = \hat{xOy} = 100^@` (hai góc đối đỉnh)

`@)` `\hat{xOy + \hat{xOy'} = 180^@`

hay `100 +` `\hat{xOy'} = 180^@`

`⇒\hat{xOy'} = 180^@ - 100^@ = 80^@`

`@)` `\hat{x'Oy} = \hat{xOy'} = 80^@` (hai góc đối đỉnh)

Ta có : 

\(\widehat{O_1}=180^o-\widehat{O_4}=180^o-100^o=80^o\)

\(\widehat{O_2}=\widehat{O_4}=100^o\) (đối đỉnh)

\(\widehat{O_3}=\widehat{O_1}=80^o\) (đối đỉnh)

a) Vì AOC + BOC = 180 độ

và BOC + BOD = 180 độ

=> AOC = BOD ( 2 góc đối đỉnh )

mà AOC = 45*

=> BOD = 45*

Vì AOD và AOC là 2 góc kề bù ( CD cắt AB tại O )

=> AOD + AOC = 180*

Thay AOC = 45*

=> AOD = 180* - 45* = 135*

b) Các cặp góc bù nhau là:

+ AOC và BOC.

+ BOC và BOD

+ BOD và AOD

+ AOD và AOC

cảm ơn bạn