cho góc bẹt \(\widehat{ABD}\).Trên cùng nửa mặt phẳng bờ AD vẽ 2 tia BC và BE sao cho \(\widehat{ABC}\)= 1120; \(\widehat{DBC}\)=340
a, tính \(\widehat{CBD}\)
b, chứng tỏ BE là tia phân giác của \(\widehat{CBD}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Sửa đề 1 tí nhé
Ta có: CBD = 180 độ - ABC
CBD = 180 độ - 112 độ
CBD = 68 độ
Ta có: ABE = 180 độ - EBD = 146 độ
=> Góc ABC < góc ABE
Theo đề ra: Tia BC và tia BE thuộc nửa mặt phẳng bờ AD
=> BC nằm giữa hai tia BA và BE
Mà: BE nằm giữa hai tia BA và BD
=> BE nằm giữa hia tia OC và BD
Ta có: Góc DBE = 34 độ
Góc CBD = 68 độ
=> Góc DBE = 1/2 góc DBC
Vậy BE là tia phân giác của góc DBC

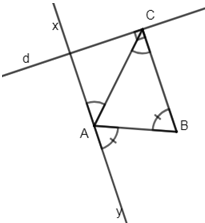
a) Ta có: mà hai góc đó là hai góc so le trong nên
suy ra (1)
mà hai góc đó là hai góc so le trong nên suy ra (2)
Từ (1) và (2) suy ra Ax và Ay cùng // BC.
Lại có tia Ax thuộc mặt phẳng bờ AB có chứa điểm C, tia Ay thuộc mặt phẳng
bờ AB không chứa điểm C
Ax và Ay là hai tia đối nhau.
b) Vì Ax và Ay là hai tia đối nhau (cmt) mà và
nên suy ra
Mà nên suy ra

a) Ta có: \(\widehat{ABC}+\widehat{CBD}=180^0\)( kề bù )
\(112^0+\widehat{CBD}=180^0\)
\(\widehat{CBD}=68^0\)
b) Ta có: \(\widehat{CBE}+\widehat{EBD}=\widehat{CBD}\)
\(\widehat{CBE}+34^0=68^0\)
\(\widehat{CBE}=34^0\)
Vậy BE là tia phân giác của góc CBD
Bài làm
~ Đề bài phải làm godc DBE = 34* mới hợp lí. ~
b) Ta có: \(\widehat{ABC}+\widehat{CBD}=180^0\) ( hai góc kề bù )
hay \(112^0+\widehat{CBD}=180^0\)
=> \(\widehat{CBD}=180^0-112^0=68^0\)
Vậy \(\widehat{CBD}=68^0\)
~ Ngoài tính theo góc kề bù, bạn có thể cộng góc AB với CBE + EBD = 180o Vì góc ABD là góc bẹt. Rồi lấy 180o - 112o - 34o thì sẽ ra góc CBE, rồi lấy góc CBE + EBD thì sẽ ra, nhưng góc kề bù sẽ tính nhanh hơn đó. ~
b) Ta có \(\widehat{CBE}+\widehat{EBD}=68^0\)
hay \(\widehat{CBE}=180^0-\widehat{EBD}\)
=> \(\widehat{CBE}=68^0-34^0\)
=> \(\widehat{CBE}=34^0\)
Mà \(\widehat{EBD}=34^0\)
=> \(\widehat{CBE}=\widehat{EBD}=34^0\)
Do đó: BE là tia phân giác của \(\widehat{CBD}\)
# Chúc bạn học tốt #

b) Ta có: tia Oz nằm giữa hai tia Ox và Ot(cmt)
nên \(\widehat{xOz}+\widehat{tOz}=\widehat{xOt}\)
\(\Leftrightarrow\widehat{tOz}+70^0=125^0\)
hay \(\widehat{tOz}=55^0\)
Ta có: \(\widehat{xOz}+\widehat{yOz}=180^0\)(hai góc kề bù)
\(\Leftrightarrow70^0+\widehat{yOz}=180^0\)
hay \(\widehat{yOz}=110^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia Oy, ta có: \(\widehat{yOt}< \widehat{yOz}\left(55^0< 110^0\right)\)
nên tia Ot nằm giữa hai tia Oy và Oz
Ta có: tia Ot nằm giữa hai tia Oy và Oz(cmt)
mà \(\widehat{yOt}=\widehat{zOt}\left(=55^0\right)\)
nên Ot là tia phân giác của \(\widehat{yOz}\)(đpcm)
a) Ta có: \(\widehat{yOt}+\widehat{xOt}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{xOt}+55^0=180^0\)
hay \(\widehat{xOt}=125^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOz}< \widehat{xOt}\left(70^0< 125^0\right)\)
nên tia Oz nằm giữa hai tia Ox và Ot(Đpcm)