\(a,F_{\left(x\right)}=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\)

\(=\left(x^2+5x+6\right)\left(x^2+5x-6\right)\)

Đặt \(x^2+5x=a\)

\(\Rightarrow F_x=\left(a+6\right)\left(a-6\right)=a^2-36\)

\(\Rightarrow F_{min}=-36\Leftrightarrow a^2=0\)

\(\Rightarrow x^2+5x=0\Rightarrow x\left(x+5\right)=0\Rightarrow\orbr{\begin{cases}x=0\\x=-5\end{cases}}\)

Vậy GTNN của \(F_x=-36\Leftrightarrow x\in\left\{0;-5\right\}\)

\(b,A=\left(1-x^n\right)\left(1+x^n\right)+\left(2-y^n\right)\left(2+y^n\right)\)

\(=1-x^{2n}+4-y^{2n}\)

\(=5-x^{2n}-y^{2n}\)

\(\Rightarrow A_{max}=5\Leftrightarrow\hept{\begin{cases}x^{2n}=0\\y^{2n}=0\end{cases}\Rightarrow\hept{\begin{cases}x=0\\y=0\end{cases}}}\)

a) x(x – y) + y(x – y) = x2 – xy + yx – y2 = x2 – xy + xy – y2 = x2 – y2

b) xn–1(x + y) – y( xn–1 + yn–1 ) = xn + xn–1y – yxn–1 – yn

= xn + xn–1y – xn–1y – yn = xn - yn

a) x (x - y) + y (x - y) = x² – xy+ yx – y²

                                = x² – xy+ xy – y²

                                = x² – y²

b) x^{n – 1} (x + y) – y(x^{n – 1} + y^{n – 1}) =xⁿ+ x^{n – 1}y – yx^{n – 1} - yⁿ

                                                    = xⁿ + x^{n – 1}y - x^{n – 1}y - yⁿ

                                                    = xⁿ – yⁿ.

a) A = (x-1)(x+2)(x+3)(x+6)

A= [(x-1)(x+6)][(x+2)(x+3)]

A=(x^2 + 5x - 6)(x^2 + 5x + 6) ( cái này mik làm tắt)

A = (x^2+5x)^2 - 6^2

A= (x^2+5x)^2 - 36

...

a, GTNN của A là 0 vì nếu x>0 thì GTNN của x là 1 mà trong A có (x-1) có thể bằng (1-1) = 0 mà 0 nhân với bất kì số nào cũng bằng 0

Chọn A.

Ta có: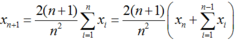 

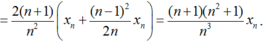
Do đó: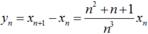 

- Ta chứng minh dãy (y_n)  tăng.

Ta có: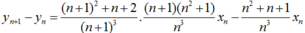 

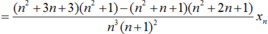
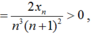
- Ta chứng minh dãy (y_n)  bị chặn.

Trước hết ta chứng minh: x_n ≤ 4(n – 1) (1)

 * Với n = 2, ta có: x₂ = 4x₁ = 4 nên (1) đúng với n = 2

 * Giả sử (1) đúng với n, tức là: x_n ≤ 4(n – 1), ta có

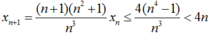
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng

Ta có: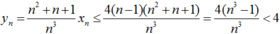 

Vậy bài toán được chứng minh.

a: ta có: \(x\left(x-y\right)+y\left(x-y\right)\)

\(=\left(x-y\right)\left(x+y\right)\)

\(=x^2-y^2\)

b: Ta có: \(x^{n-1}\left(x+y\right)-y\left(x^{n-1}+y^{n-1}\right)\)

\(=x^n+x^{n-1}\cdot y-x^{n-1}\cdot y-y^n\)

\(=x^n-y^n\)

1.

$x(x+2)(x+4)(x+6)+8$

$=x(x+6)(x+2)(x+4)+8=(x^2+6x)(x^2+6x+8)+8$

$=a(a+8)+8$ (đặt $x^2+6x=a$)

$=a^2+8a+8=(a+4)^2-8=(x^2+6x+4)^2-8\geq -8$

Vậy $A_{\min}=-8$ khi $x^2+6x+4=0\Leftrightarrow x=-3\pm \sqrt{5}$

2.

$B=5+(1-x)(x+2)(x+3)(x+6)=5-(x-1)(x+6)(x+2)(x+3)$

$=5-(x^2+5x-6)(x^2+5x+6)$

$=5-[(x^2+5x)^2-6^2]$

$=41-(x^2+5x)^2\leq 41$

Vậy $B_{\max}=41$. Giá trị này đạt tại $x^2+5x=0\Leftrightarrow x=0$ hoặc $x=-5$

 4-3=2( dân chơi mới hiểu)

Chắc là viết thiếu số "1" đấy, sợ lớp 11 còn chưa làm được cơ