Cho Q= 2x2 - 6x
Hãy tìm giá trị nhỏ nhất của Q.
Trả lời và giải thích hộ tui nhe. Tks
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
18 tháng 12 2016
a) 10,5 : 3,5 = 3
-> số tự nhiên lớn nhất là 2 thì 3.5 x 2 < 10,5
b) 30,15 : 6,26 \(\approx\)4,8
-> số tự nhiên bé nhất là 5 thì 6,26 x 5 > 30,15
11 tháng 7 2019
a) Ta có: \(\left|x+\frac{3}{2}\right|\ge0\forall x\)
Hay : P \(\ge\)0 \(\forall\)x
Dấu "=" xảy ra khi: \(x+\frac{3}{2}=0\) <=> \(x=-\frac{3}{2}\)
Vậy Pmin = 0 tại x = -3/2
b) Ta có: \(\left|3-x\right|\ge0\forall x\)
=> \(\left|3-x\right|+\frac{2}{5}\ge\frac{2}{5}\forall x\)
hay P \(\ge\)2/5 \(\forall\)x
Dấu "=" xảy ra khi: 3 - x = 0 <=> x = 3
Vậy Pmin = 2/5 tại x = 3
11 tháng 7 2019
a)Có giá trị tuyệt đối của x+3/2 >=0 với mọi x
=> P>=0 với mọi x
P=0 khi x+3/2=0 <=> x=-3/2
Vậy P có giá trị nhỏ nhất là 0 khi x=-3/2
CM
28 tháng 1 2019
Đáp án C
Lưu ý: Đề không cho tìm max – min trên đoạn nên ta không thể so sánh các giá trị như vậy
Cách giải: Lập BBT và ở đây kết luận được giá trị nhỏ nhất của hàm số là 1 , nhưng hàm số không có giá trị lớn nhất.
CM
31 tháng 7 2017
Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Ta có bảng biến thiên sau:
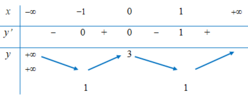
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.
KN
0
NQ
0
17 tháng 4 2017
\(\frac{10n-3}{4n-3}\)=\(\frac{10n-6+3}{5n-3-n}\)=\(\frac{2\left(5n-3\right)+3}{5n-3-n}\)=2+\(\frac{3}{5n-3-n}\)
vậy 10n-3/4n-3 lớn nhất khi \(\frac{3}{5n-3-n}\)lớn nhất
khi 5n-3-n bé nhất
5n-3-n=4n-3 bé nhất
4n-3 là số nguyên dương bé nhất =>4n-3=1
n=4
Q= 2x2 - 6x
= 2 ( x2 - 3x )
= 2 ( x2 - 2x.3/4 + 9/16 ) - 9/8
= 2 (x - 3/4 ) 2 - 9/8 >= -9/8 với mọi x
dấu = xảy ra khi và chỉ khi x- 3/4 = 0
x=3/4
vậy min Q = -9/8 khi và chỉ khi x=3/4
#mã mã#
Cấn lắm 1 lời giải thích là vì sao lại làm như vậy