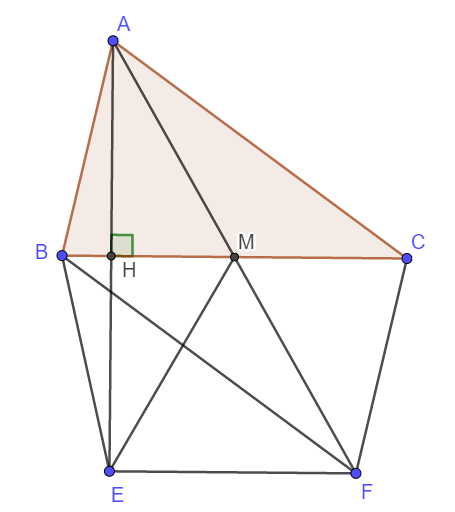
Cho tam giác ABC có AH vông góc với BC (H thuộc BC), M là trung điểm của BC. Trên tia đối của tia HA lấy điểm E sao cho HA = HE. Trên tia đối của tia MA lấy điểm F sao cho MA = MF. C/minh:
a) ME =MF.
b) BE = CF.
c) AC//BF.
d) EF//BC.
Giúp mình nhanh với nhé!


a) Xét 2 \(\Delta\) vuông \(AHM\) và \(EHM\) có:
\(\widehat{AHM}=\widehat{EHM}=90^0\)
\(AH=EH\left(gt\right)\)
Cạnh HM chung
=> \(\Delta AHM=\Delta EHM\) (2 cạnh góc vuông tương ứng bằng nhau)
=> \(AM=EM\) (2 cạnh tương ứng)
Mà \(AM=MF\left(gt\right)\)
=> \(EM=MF.\)
b) Theo câu a) ta có \(\Delta AHM=\Delta EHM.\)
=> \(\widehat{AMH}=\widehat{EMH}\) (2 góc tương ứng)
Mà \(\widehat{AMH}=\widehat{FMC}\) (vì 2 góc đối đỉnh)
=> \(\widehat{EMH}=\widehat{FMC}\)
hay \(\widehat{EMB}=\widehat{FMC}.\)
Xét 2 \(\Delta\) \(BME\) và \(CMF\) có:
\(BM=CM\) (vì M là trung điểm của \(BC\))
\(\widehat{BME}=\widehat{CMF}\left(cmt\right)\)
\(ME=MF\left(cmt\right)\)
=> \(\Delta BME=\Delta CMF\) (c . g . c)
=> \(BE=CF\) (2 cạnh tương ứng)
c) Xét 2 \(\Delta\) \(AMC\) và \(FMB\) có:
\(AM=FM\left(gt\right)\)
\(\widehat{AMC}=\widehat{FMB}\) (vì 2 góc đối đỉnh)
\(MC=MB\) (như ở trên)
=> \(\Delta AMC=\Delta FMB\) (c . g . c)
=> \(\widehat{ACM}=\widehat{FBM}\) (2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong
=> \(AC\) // \(BF.\)
Còn câu d) thì mình đang nghĩ nhé bạn.
Chúc bạn học tốt!