Nối NQ. 

Vì NPQM là hình thoi

=> \(\widehat{MQP}=\widehat{MNP}=120^o\)

=> \(\widehat{NQF}=\frac{1}{2}.\widehat{MQP}=60^o\)

Có tam giác NMQ cân tại M  ( NM=MQ)

\(\widehat{MNQ}=\frac{1}{2}\widehat{MNP}=\frac{1}{2}.120=60^o\)

=> Tam giác NMQ đều

Xét tam giác NME và tam giác NQF 

có: NM=NQ  ( tam giác NMQ đều)

    ME =QF ( giả thiết)

   \(\widehat{NME}=\widehat{NQF}=60^o\)

=> Tam giác NME = Tam giác NQF

=> NE =NF => Tam giác NEF cân tại N

và \(\widehat{MNE}=\widehat{QNF}\)=> ^QNF+ ^QNE =^MNE +^QNE =^QNM =60^o

=> \(\widehat{FNE}=60^o\)

=> Tam giác NEF  đều

Gợi ý thôi cx được nhưng mà gợi ý theo kiểu chi tiết nhé , đừng bảo là kẻ cái này cái nọ rồi tự giải thì mik chịu :D 

Nhanh nhé , làm xong , mik sẽ

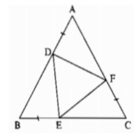
Ta có: AB = AD +DB (1)

BC = BE + EC (2)

AC = AF + FC (3)

AB = AC = BC ( vì tam giác ABC là tam giác đều) (4)

AD = BE = CF ( giả thiết) (5)

Từ (1), (2), (3) và (4),(5) suy ra: BD = EC = AF

Xét ΔADF và ΔBED, ta có:

AD = BE (gt)

∠A =∠B =60o (vì tam giác ABC đều)

AF = BD (chứng minh trên)

suy ra: ΔADF= ΔBED (c.g.c)

⇒ DF=ED (hai cạnh tương ứng) (6)

Xét ΔADF và ΔCFE, ta có:

AD = CF (gt)

∠A =∠C =60o (vì tam giác ABC đều)

AF = CE (chứng minh trên)

suy ra: ΔADF= ΔCFE (c.g.c)

Nên: DF = FE (hai cạnh tương ứng) (7)

Từ (6) và (7) suy ra: DF = ED = FE

Vậy tam giác DFE đều

do tam giác abc cân tại a

=>góc abc=180-2*góc a

do am=an

=>tam giác amn can taị a

=>góc amn=180-2*góc a

=>góc amn=góc abc(vì cùng bằng 

180-2*góc a)

mà hai góc này ở vị trí so le trong 

=>mn song song vs ab

xét 2 tam giác abn và acm có

chung góc a

am=an

ab=ac

=>tg abn=tg acm

=>bm=cm(2 cạnh tương ứng)

cau 2

theo đề bài ta có

tg abc đều =>ab=bc=ca

ad=be=cf

=>ab-ad=bc-be=ac-cf

hay bd=ce=af

xét 3 tg ade,bed và cef ta có

góc a=gócb=gócc

ad=be=cf

bd=ce=af

=> tg ade= tg bed= tg cef 

=>de=df=ef

=>tg def là tg đều

\(\Delta ABC\)đều (gt) nên AB = BC = AC ; góc A = góc B = góc C = 60⁰ mà AD = BE = CF (gt)

=> AB - AD = BC - BE = AC - CF <=> BD = CE = AF

\(\Delta ADF,\Delta BED\)có AD = BE (gt) ; góc DAF = góc EBD = 60⁰ (cmt) ; AF = BD (cmt) nên\(\Delta ADF=\Delta BED\left(c.g.c\right)\)

=> DF = ED (2 cạnh tương ứng) (1)

\(\Delta ADF,\Delta CFE\)có AD = CF (gt) ; góc DAF = góc FCE = 60⁰ (cmt) ; AF = CE (cmt) nên\(\Delta ADF=\Delta CFE\left(c.g.c\right)\)

=> DF = FE (2 cạnh tương ứng) (2).Từ (1) và (2),ta có DF = FE = ED.Vậy\(\Delta DEF\)đều

. Cho tam giác ABC, Các tia phân giác của các góc B và C cắt nhau tại I Qua I kẻ đường thẳng song song với BC cắt AB tại M và AC tại N. Chứng minh rằng MN = BM + CN

Hình tự vẽ

Xét 3 tam giác \(ADF,BED,CFE\),ta có:

\(AD=BE=CF\)(gt )

\(\widehat{A}=\widehat{B}=\widehat{C}\)(gt)

DB=EC=AD ( do các cạnh của tam giác đều ABC - các cạnh AD,BE,FC = nhau )

=>3 tam giác \(ADF,BED,CFE\)=nhau

=> DE=DF=FE

=> tam giác DEF đều

P/s tham khảo nha

Ta có: AB=BC=CA (t/g ABC đều)

AD=BE=CF

=>BD=CE=AF

Xét t/g ADF và t/g BED có:

AD=BE (gt)

góc A=góc B = 60 độ (gt)

AF=BD (cmt)

=>t/g ADF = t/g BED (c.g.c)

=>DF = DE (1)

Xét t/g ADF và t/g CFE có:

AD = CF (gt)

góc A=góc C = 60 độ (gt)

AF = CE (cmt)

=>t/g ADF = t/g CFE (c.g.c)

=> DF = EF (2)

Từ (1) và (2) => DF = DE = EF => t/g DEF đều