Cho tam giác ABC vuông tại A , có BC = 10, AC =8cm trên cạnh AB sao cho BM=4cm . D là điểm sao cho A là trung điểm của CD . Gọi N là trung điểm của BD . Chứng minh rằng C, M ,N thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

LH
9 tháng 5 2017
a. Xét tam giác ABC \(⊥\) A
BC2=AB2+AC2 (Pytago)
102=82+AC2 => AC=10cm
b. Xét tam giác BCD có \(\frac{BM}{AB}=\frac{\frac{16}{3}}{8}=\frac{2}{3}\)
=> M là trực tâm cuả tam giác BCD
c. Ta có: DM là đttuyến của tam giác BCD mà DE cũng là đttuyến của tam giác BCD ( BE=CE)
=> DM trùng DE=> D, M, E thẳng hàng

25 tháng 3 2023
a: AM=6-2=6cm
AN=12-3=9cm
=>AM/AB=AN/AC
=>MN//BC
b: Xet ΔAKC có NI//KC
nên NI/KC=AI/AK
Xét ΔABK có MI//BK
nên MI/BK=AI/AK
=>NI/KC=MI/BK
c: NI/KC=MI/BK
KC=KB
=>NI=MI
=>I là tđ của MN
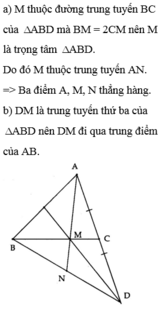
Hinh ban tu ve nhe
Ta ke duong trung tuyen DE ,goi giao diem cua DE va AB la Q
Ta co:\(AB=\sqrt{BC^2-AC^2}=\sqrt{100-64}=\sqrt{36}=6\left(cm\right)\)
Suy ra:\(MA=2\left(cm\right)\left(1\right)\)
Hay Q la trong tam cua \(\Delta BCD\)
Co \(\frac{BQ}{AB}=\frac{2}{3}\Rightarrow BQ=4\left(cm\right)\)
\(\Rightarrow AQ=2\left(cm\right)\left(2\right)\)
Tu (1) va (2) suy ra:\(AQ=AM\)
Vi \(M,Q\in AB\)va \(AQ=AM\) suy ra:\(M\equiv Q\)
Nen M la diem dong quy trong \(\Delta BCD\)
Hay 3 diem M,N,C thang hang.
:)