Để phương trình có nghiệm thì : 

\(\Delta_x=a^2-\left(2a^2+b^2-5\right)\ge0\)

\(\Leftrightarrow a^2+b^2\le5\)

\(\Leftrightarrow\left(a+b\right)^2\le5+2ab\)

\(\Leftrightarrow ab\ge\frac{\left(a+b\right)^2-5}{2}\)

Ta có :

\(P=\left(a+1\right)\left(b+1\right)=ab+a+b+1\)

\(\ge\frac{\left(a+b\right)^2-5}{2}+\left(a+b\right)+1=\frac{1}{2}\left(a+b+1\right)^2-2\ge-2\)

Dấu " = " xảy ra khi \(\hept{\begin{cases}a=-2\\b=1\end{cases}}\)

Đa thức có nghiệm \(\Rightarrow\Delta'=a^2-\left(2a^2+b^2-5\right)\ge0\)

\(\Rightarrow a^2+b^2\le5\)

\(P=\left(a+1\right)\left(b+1\right)=ab+a+b+1=\dfrac{\left(a+b\right)^2-\left(a^2+b^2\right)}{2}+a+b+1\)

\(P\ge\dfrac{\left(a+b\right)^2-5}{2}+a+b+1=\dfrac{1}{2}\left(a+b+1\right)^2-2\ge-2\)

\(P_{min}=-2\) khi \(\left\{{}\begin{matrix}a^2+b^2=5\\a+b+1=0\end{matrix}\right.\) \(\Rightarrow\left(a;b\right)=\left(2;-1\right);\left(-1;2\right)\)

Đáp án C.

Đáp án B

Ta có

f ' x = 3 x + a 2 + x + b 2 − x 2 = 3 x 2 + 2 a + b x + a 2 + b 2

Để hàm số luôn đồng biến trên − ∞ ; + ∞

thì Δ ' = a + b 2 − a 2 + b 2 ≤ 0 ⇔ a b ≤ 0

Ta có  

P = a 2 + b 2 − 4 a − 4 b + 2 = a + b − 2 2 − 2 a b − 2 ≥ − 2.

Dâu bằng xảy ra khi a + b = 2 a b = 0 ⇔ a = 2 b = 0  hoặc ngược lại.

bài 5 nhé:

a) (a+1)²>=4a

<=>a²+2a+1>=4a

<=>a²-2a+1.>=0

<=>(a-1)²>=0 (luôn đúng)

vậy......

b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:

a+1>=\(2\sqrt{a}\)

tương tự ta có:

b+1>=\(2\sqrt{b}\)

c+1>=\(2\sqrt{c}\)

nhân vế với vế ta có:

(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)

<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)

<=>(a+)(b+1)(c+1)>=8 (vì abc=1)

vậy....

bạn nên viết ra từng câu

Chứ để như thế này khó nhìn lắm

Đáp án B

Ta có: f ' x = − 3 x 2 + 3 x + a 2 + 3 x + b 2 = 3 x 2 + 6 a + b x + 3 a 2 + 3 b 2  

Để hàm số đồng biến trên − ∞ ; + ∞  thì f ' x ≥ 0 ∀ x ∈ − ∞ ; + ∞  

⇔ 3 x 2 + 6 a + b x + 3 a 2 + 3 b 2 ≥ 0 ∀ x ∈ ℝ ⇔ x 2 + 2 a + b x + a 2 + b 2 ≥ 0 ∀ x ∈ ℝ ⇔ Δ ' = a + b 2 − a 2 + b 2 ≤ 0 ⇔ 2 a b ≤ 0 ⇔ a b ≤ 0  

TH1:   b = 0 ⇒ P = a 2 − 4 a + 2 = a − 2 2 − 2 ≥ − 2 1

TH2: a > 0 , b < 0 ⇒ P = a − 2 2 + b 2 + − 4 b − 2 > − 2 2  

Từ (1) và (2) ⇒ P min = − 2   k h i   a = 0  hoặc b = 0.

Chọn đáp án D

Ta có

Suy ra

Từ giả thiết ta có f ' x + f ' ' x = 10 e x  

Để phương trình  f ' x + f ' ' x = 10 e x có nghiệm

⇔  Phương trình (*) có nghiệm

* Nếu b = 0 thì S = a 2 ≥ 10  

* Nếu b ≠ 0 thì S = a 2 - 2 a b + 3 b 2 ≥ 10 . a b 2 - 2 . a b + 3 a b 2 + 1 .

Đặt t = a b t ∈ R , suy ra S ≥ 10 . t 2 - 2 t + 3 t 2 + 1 .

Xét hàm số f t = t 2 - 2 t + 3 t 2 + 1  trên R.

Ta có

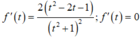
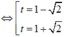
Bảng biến thiên:

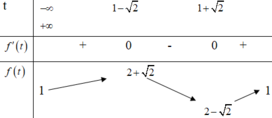
Quan sát bảng biến thiên ta thấy  f t ≥ 2 - 2