Tất cả góc đều bằng 45 độ

giai ra dc ko bn

các cặp góc đối đỉnh là \(\widehat{xOy}và\widehat{x'Oy'}\) ;\(\widehat{x'Oy}=\widehat{xOy'}\)

ta có  \(\widehat{xOy}và\widehat{x'Oy'}\) là 2 góc đối đỉnh \(\Rightarrow\text{ }\text{ }\widehat{xOy}=\widehat{x'Oy'}=45độ\)

ta có \(\widehat{x'Oy}+\widehat{xOy}=180độ\)

\(\Rightarrow\widehat{x'Oy}+45độ=180độ\)

\(\Rightarrow\widehat{x'Oy}=180độ-45độ=135độ\)

ta có \(\widehat{x'Oy}=\widehat{xOy'}\) là 2 góc đối đỉnh

\(\Rightarrow\widehat{x'Oy}=\widehat{xOy'}=135độ\)

vậy \(\widehat{x'Oy}=135độ;\widehat{xOy'}=135độ;\widehat{x'Oy'}=45độ\)

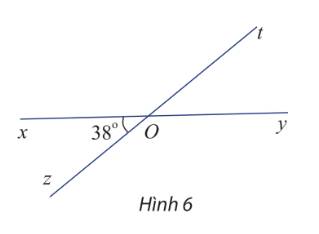
Ta có hai góc \(\widehat {xOz}\) và \(\widehat {tOy}\) đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 38^\circ \)

hai góc \(\widehat {xOt}\) và \(\widehat {yOz}\) đối đỉnh nên \(\widehat {xOt} = \widehat {yOz}\)

\(\widehat {xOz}\) và \(\widehat {xOt}\) bù nhau nên \(\widehat {xOt} = 180^\circ  - \widehat {xOz} = 180^\circ  - 38^\circ  = 142^\circ \)

Vậy \(\widehat {xOz} = \widehat {tOy} = 38^\circ \) và \(\widehat {xOt} = \widehat {yOz} = 142^\circ \)

ta có:\(\widehat{aOb}\) = 180

\(\Rightarrow\)3 x \(\widehat{aOc}\)=180

\(\Rightarrow\)\(\widehat{aOc}\)=180 : 3 = 60

\(\Rightarrow\)\(\widehat{aOc}\)=\(\widehat{bOd}\)= 60 (2 góc đối đỉnh)

ta có: \(\widehat{aOc}\)+\(\widehat{cOb}\)= 180 (2 góc kề bù)

\(\Rightarrow\)60 + \(\widehat{cOb}\)= 180

\(\Rightarrow\)\(\widehat{cOb}\)= 180 - 60 = 120

\(\Rightarrow\)\(\widehat{aOd}\)=\(cOb\)= 120 (2 goc đối đỉnh)

Vậy \(\widehat{aOc}\)= 60;\(\widehat{cOb}\)= 120;\(\widehat{bOd}\)= 60;\(\widehat{aOd}\)=120

cảm ơn bạn

Vì xOb và xOa kề bù 

\(\Rightarrow\widehat{xOb}+\widehat{xOa}=180^o\left(kb\right)\)

\(\Rightarrow48^o+\widehat{xOa}=180^o\Leftrightarrow\widehat{xOa}=180^o-48^o=132^o\)

Vì xOb và aOy đối đỉnh 

\(\Rightarrow\widehat{xOb}=\widehat{aOy}=48^o\)

Vì xOa và yOb đổi đính

\(\Rightarrow\widehat{xOa}=\widehat{yOb}=132^o\)

các cậu còn lại tương tự

Các bạn giúp mình với ạ

40  độ

mình cũng nghĩ vậy