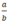Theo đề bài, ta có : a/b với a,b \(\in\) Z, b < 0

a) khi a và b cùng dấu mà b > 0  thì a > 0. Do đó số hữu tỉ a/b > 0

b) Khi a và b khác dấu mà b > 0 do đó a < 0. Do đó số hữ tỉ là : a/b < 0

Khi a và b cùng dấu mà a > 0; b > 0 thì \(\frac{a}{b}>0\)

Khi a và b khác dấu mà a < 0; b > 0 thì \(\frac{a}{b}< 0\)

Với a, b ∈ Z, b> 0

- Khi a , b cùng dấu thì  > 0

- Khi a,b khác dấu thì  < 0

Tổng quát: Số hữu tỉ   ( a,b ∈ Z, b # 0) dương nếu a,b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu

a = 0

Với a, b ∈ Z; b ≠ 0 thì:

- Khi a, b cùng dấu thì 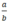 > 0

- Khi a, b khác dấu thì 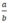 < 0

Tổng quát: Số hữu tỉ 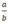 (a, b ∈ Z; b ≠ 0) > 0 nếu a, b cùng dấu; < 0 nếu a, b khác dấu; = 0 nếu a = 0.

Nếu a,b cùng dấu thì \(\dfrac{a}{b}\ge0\)

Nếu a,b khác dấu thì \(\dfrac{a}{b}< 0\)

\(\left[{}\begin{matrix}a\ge0,b>0\\a\le0,b< 0\end{matrix}\right.\Rightarrow\dfrac{a}{b}\ge0\\ \left[{}\begin{matrix}a\ge0,b< 0\\a\le0,b>0\end{matrix}\right.\Rightarrow\dfrac{a}{b}\le0\)

Khi a,b cùng dấu thì \(\frac{a}{b}>0\) ; khác dấu thì \(\frac{a}{b}< 0\)

Số nguyên a là số hữu tỉ vì ta có thể viết a = \(\frac{a}{1}\)

3. Với a, b ∈ Z, b # 0
- Khi a, b cùng dấu thì a/b > 0
- Khi a, b khác dấu thì a/b < 0
Kết luận: Số hữu tỉ a/b (a, b ∈ Z, b # 0) dương nếu a, b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu a = 0.

Nếu a/b cùng dấu thì a/b luôn dương => a/b > 0

Nếu a/b trái dấu thì a/b luôn âm => a/b < 0

Học tốt

bạn vào link https://alfazi.edu.vn/question/5b78c797e5cde951c7e8307d Tham gia trả lời câu hỏi để nhận được những phần quà hấp dẫn đến từ Alfazi như: xu, balo, áo, giày,... và các dụng cụ học tập khác nhé

Rồi bạn trả lời"được bạn My Love mời"cám ơn bn

Ta có : 

Khi a, b cùng dấu :

Nếu a > 0 và b > 0 suy ra : 

Nên :  vậy  

Nếu a < 0 và b < 0 suy ra : 

Nên :  vậy  

Khi a, b khác dấu :

Nếu a > 0 và b < 0 suy ra : 

Nên :  vậy  

Nếu a < 0 và b > 0 suy ra : 

Nên :  vậy  

a, b cùng dấu thì a/b > 0 ..dễ hiểu thôi nếu cả a, b đều dương thì a/d dĩ nhiên dương, nếu cả a,b đều âm thì a/b cũng dương vì -a/-b = a/b (nhân hai vế với trừ 1) 
a, b khác dấu thì a/b luôn âm nên a/b < 0