có bài toán hình mình không giải được nên nhờ ad giải hộ nè, bài toán như sau: "Cho tam giác đều ABC có điểm M nằm trong tam giác đó, biết MA mũ 2=MB mũ 2+MC mũ 2. Tính góc BMC".
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phía nửa mặt phẳng bờ AB không chứa M lấy điểm N sao cho AMN là tam giác đều
Ta có ˆCAB=ˆMANCAB^=MAN^
<=>ˆCAM+ˆMAB=ˆMAB+ˆBANCAM^+MAB^=MAB^+BAN^
<=>ˆCAM=ˆBANCAM^=BAN^ (1)
mà CA =BA và AM =AN (2)
từ (1, 2) =>△CAM=△BAN△CAM=△BAN (c, g, c) (3)
(3) =>CM =BN
ta có MA2=MB2+MC2MA2=MB2+MC2
<=>MN2=MB2+BN2MN2=MB2+BN2
=>t giác MBN vuông tại B
(3) =>ˆACM=ˆABNACM^=ABN^
ˆMBN=ˆABM+ˆABN=90∘MBN^=ABM^+ABN^=90∘
<=>ˆABM+ˆACM=90∘ABM^+ACM^=90∘
<=>(60∘−ˆMBC)+(60∘−ˆMCB)=90∘(60∘−MBC^)+(60∘−MCB^)=90∘
<=>ˆMBC+ˆMCB=30∘MBC^+MCB^=30∘
<=>ˆBMC=180∘−30∘=150∘

- Thứ tự sắp xếp là 5, 1, 2, 4, 3
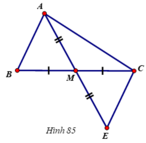
Tam giác AMB và tam giác EMC có
MB = MC (gt)
MA = ME (gt)
Do đó ΔAMB = ΔEMC (c.g.c)


Em tham khảo nhé!
Câu hỏi của channel Anhthư - Toán lớp 7 - Học toán với OnlineMath
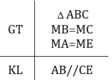
 5) Tam giác AMB và tam giác EMC có
5) Tam giác AMB và tam giác EMC có