giả bài toán sau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài toán : Mua 4 quyển vở hết 8000 đồng . Hỏi mua 3 quyển vở hết bao nhiêu tiền ?
Bài giải
Mua 1 quyển vở hết số tiền là
8000 : 4 = 2000 ( đồng )
Mua 3 quyển vở hết sô tiền là
2000 x 3 = 6000 ( đồng )
Đáp số 6000 đồng

Đề toán: Mai mua 4 hộp bút giá 8000 đồng, Hùng cũng mua 3 hộp bút cùng loại. Hỏi Hùng cần phải trả bao nhiêu tiền?
Bài giải:
Một hộp bút đó có giá là:
8000 : 4 = 2000 (đồng)
Hùng cần phải trả số tiền là:
2000 x 3 = 6000 (đồng)
Đáp số: 6000 đồng

Số tiền mua cá là:
88 000 : (6 + 5) x 6 = 48000 (đồng)
Đáp số: 48000 đồng.

Bài 7:
#include <bits/stdc++.h>
using namespace std;
double a,b,c;
int main()
{
cin>>a>>b>>c;
if ((a+b>c) && (a+c>b) && (b+c>a)) cout<<"Day la ba canh trong mot tam giac";
else cout<<"Day khong la ba canh trong mot tam giac";
return 0;
}

a)
Chọn hệ trục tọa độ như Hình 9 (vị trí rơi của cầu thuộc trục hoành và vị trí cầu rời mặt vợt thuộc trục tung).
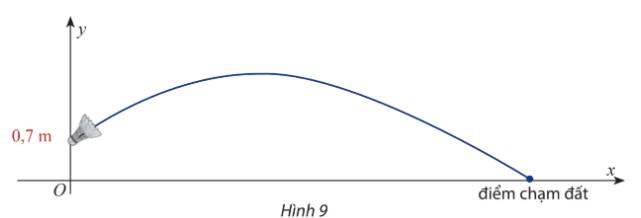
Với \(g = 9,8\;m/{s^2}\), góc phát cầu \(\alpha = {30^o}\), vận tốc ban đầu \({v_0} = 12\;m/s\), phương trình quỹ đạo của cầu là:
\(y = \frac{{ - 9,8}}{{{{2.12}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7 = - \frac{{4,9}}{{108}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7\)
Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên giải phương trình \( - \frac{{4,9}}{{108}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7 = 0\) ta được \({x_1} \approx - 1,11\) và \({x_2} \approx 13,84\)
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 13,84 m > 13,4 m (chiều dài cả sân)
Vậy lần phát cầu đã bị hỏng vì điểm rơi của cầu nằm ngoài đường biên ngoài.
b)
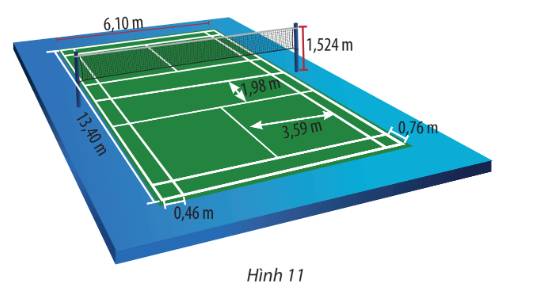
Ta so sánh tung độ của điểm trên quỹ đạo (có hoành động bằng khoảng cách từ điểm phát cầu đến chân lưới phân cách) với chiều cao mép trên của lưới.
Với \(g = 9,8\;m/{s^2}\), góc phát cầu \(\alpha = {30^o}\), vận tốc ban đầu \({v_0} = 8\;m/s\), vị trí phát cầu cách mặt đất 1,3 m. Phương trình quỹ đạo của cầu là:
\(y = \frac{{ - 9,8}}{{{{2.8}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3 = - \frac{{4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3\)
Khi \(x = 4,\)ta có \(y = - \frac{{4,9}}{{48}}{.4^2} + \frac{{\sqrt 3 }}{3}.4 + 1,3 \approx 1,98 > 1,524\)
Vậy quỹ đạo của cầu cao hơn mép trên của lưới.
Tiếp theo ta kiểm tra vị trí cầu rơi có vượt đường biên ngoài hoặc chưa tới đường biên trong hay không.
Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên giải phương trình \(y = \frac{{ - 9,8}}{{{{2.8}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3 = - \frac{{4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3\) ta được \({x_1} \approx - 1,73\) và \({x_2} \approx 7,38\)
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 7.38 m.
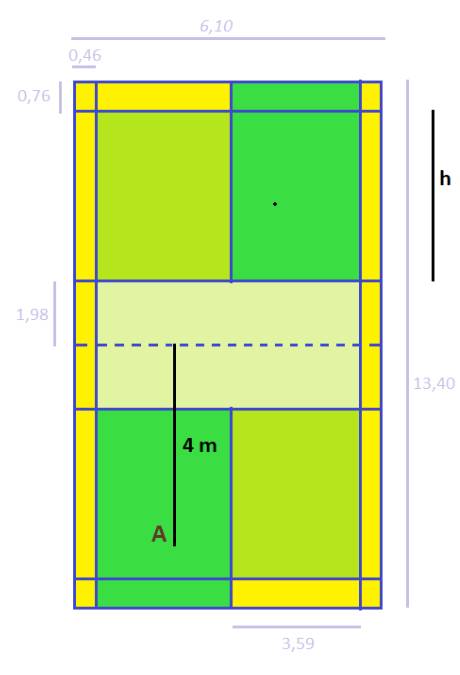
Dễ thấy: độ dài h (chiều dài của khu vực hợp lệ) là: \(13,4:2 - 1,98 -0,76= 3,96\) (m).
Do đó lần phát là hợp lệ nếu khoảng cách từ vị trí phát đến điểm rơi thuộc khoảng \(4 + 1,98 = 5,98(m)\) và \(4 + 1,98 +3,96= 9,94(m)\) và \(5,98 < 7,38 < 9,94\).
Như vậy vị trí quả cầu trên mặt đất nằm giữa đường biên trong và đường biên ngoài.
Kết luận: lần phát cầu này được coi là hợp lệ.

- Thứ tự sắp xếp là 5, 1, 2, 4, 3
Tam giác AMB và tam giác EMC có
MB = MC (gt)
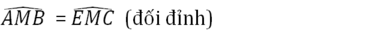
MA = ME (gt)
Do đó ΔAMB = ΔEMC (c.g.c)


- Trước hết, tốc độ gia tăng thực sự rất lớn ngoài sức tưởng tượng, thấy được việc hạn chế gia tăng dân số là đòi hỏi tất yếu cho sự phát triển của loài người. Loài người cần phải làm một việc gì đó để quyết định sự tồn tại của mình. Nếu không hạn chế sự gia tăng dân số thì con người sẽ tự làm hại chính mình.
- Điều làm cho tác giả “sáng mắt” là sự gia tăng dân số trong thời hiện đại nó đã được đặt ra từ ý nghĩa của một bài toán thời cổ đại.
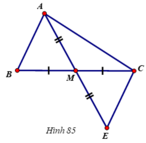
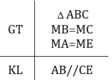
 5) Tam giác AMB và tam giác EMC có
5) Tam giác AMB và tam giác EMC có
Không biết làm phần c ==*
a) Vì \(\hept{\begin{cases}AM⊥MN\\DN⊥MN\end{cases}}\)=> AM // DN
b) Ta có : \(\widehat{A}+\widehat{ADN}=180^o\left(\text{2 góc so le trong}\right)\)mà \(\widehat{A}=40^o\)
\(\Rightarrow40^o+\widehat{ADN}=180^o\)\(\Rightarrow\widehat{ADN}=180^o-40^o=140^o\)