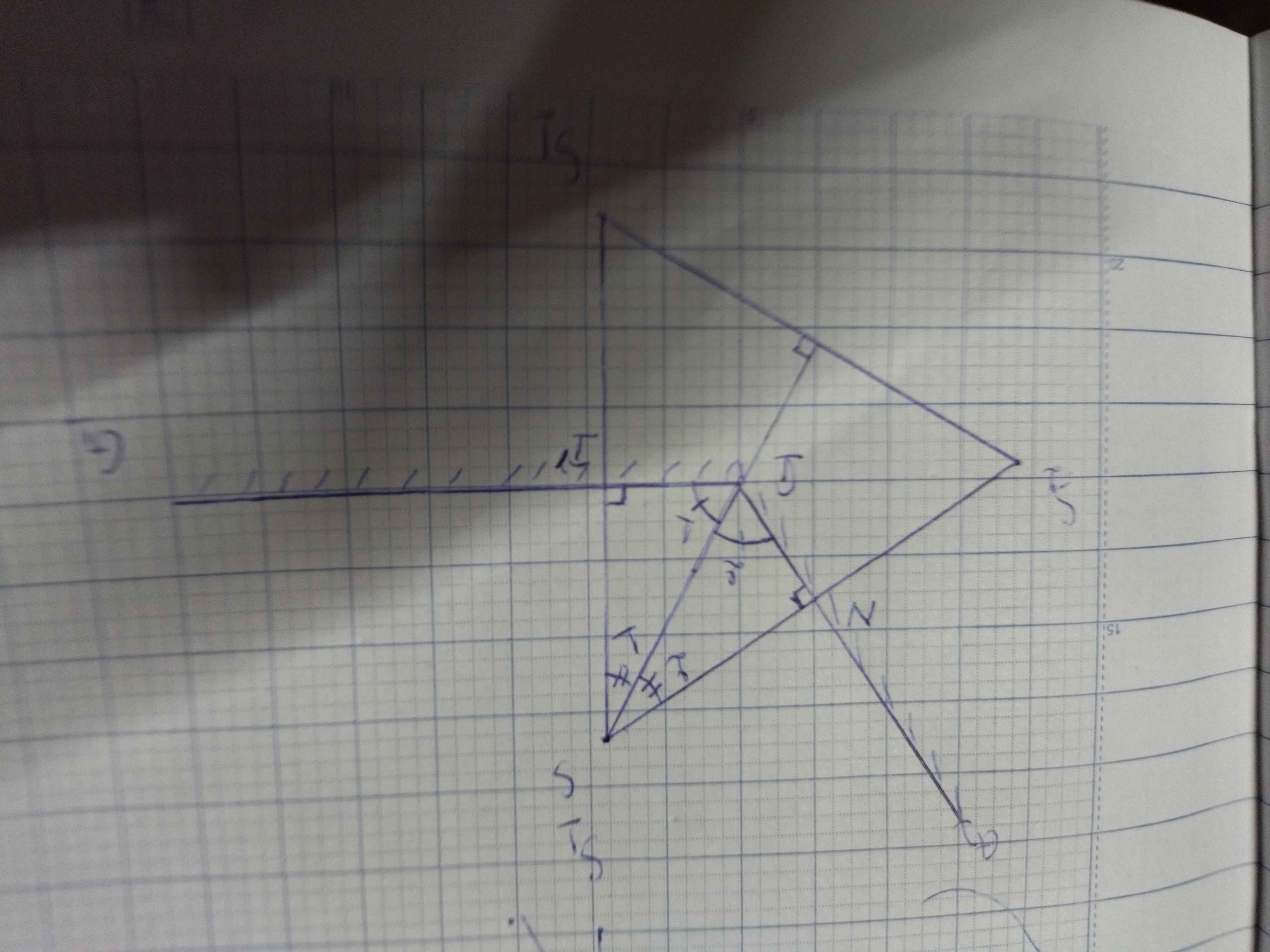
gương phẳng giao nhau tại điểm O có mặt phản xạ hợp với nhau một góc α. trên mặt phẳng phân giác của góc α có nguồn sáng điểm S cách O một khoảng a không đổi. chứng minh rằng khoảng cách giữa hai ảnh ảo đầu tiên (1 qua gương thứ nhất , 1 qua gương thứ 2 )có giá trị như nào đối với hai chiều dài hai trường hợp α= 60o và α=120o
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.Nếu giữ nguyên tia tới và quay gương góc 10 độ thì tia phản xạ quay một góc 20 độ.
2.Phải quay gương một góc 30 độ theo chiều từ trái qua phải.
3.Góc a giữa 2 gương là khoảng 60 độ.
a)tia phản xạ quay 1 góc 20 độ
b)quay gương 1 góc 30 độ theo chiều từ trái qua phải
c)góc a giữa 2 gương là khoảng 60 độ

Cách vẽ:
Gọi: S' là ảnh của S qua gương 1.
\(\Rightarrow\) Tia tới qua gương 1 tạo ra tia phản xạ đi qua S'.
Gọi: S'' là ảnh của S qua gương 2.
\(\Rightarrow\) Tia tới khi qua gương 2 cho tia phản tạo ta tia phản xạ đi qua S
\(\Rightarrow\) Tia tới sẽ đi qua S''.
Giả sử S', S'' cắt G tại A và G' tại B.
\(\Rightarrow\) SABS là đường truyền tia sáng cần vẽ.
Chứng minh:
Ta có: \(\left\{{}\begin{matrix}\widehat{SAG}=\widehat{OAB}\\\widehat{OBA}=\widehat{SBG'}\end{matrix}\right.\)
\(\widehat{ASB}+\widehat{SAB}+\widehat{SBA}=90^0\)
\(\widehat{SAB}+2\widehat{OAB}=180^0\) \(\Rightarrow\widehat{SAB}=180^0-2\widehat{0AB}\)
\(\widehat{SBA}+2\widehat{OAB}=180^0\Rightarrow\widehat{SBA}=180^0-2\widehat{OAB}\)
\(\Rightarrow\widehat{ASB}+180^0-2\widehat{0AB}+180^0-2\widehat{OBA}=180^0\)
\(\Leftrightarrow\widehat{ASB}+2\left(180^0-\widehat{0AB}-\widehat{0BA}\right)=180^0\)
\(\Leftrightarrow\widehat{ASB}+2\alpha=180^0\)
\(\Rightarrow\widehat{ASB}=180^0-2\alpha\)
Vậy \(\widehat{ASB}\) không phụ thuộc vào góc tới mà phụ thuộc vào góc hợp bởi 2 gương (đpcm).

bạn làm theo công thức số ảnh bằng 360 độ chia góc a rồi trừ đi 1