Gọi s là tập hợp các số nguyên x thỏa mãn đẳng thức |x+1| + |x-10| = 11. Tính số phần tử của tập S.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có VT = |x+1|+|x-10|
= |x+1| + |10-x| > |x+1+10-x| = 11
đẳng thức |x+1| + |x-10| = 11 <=> VT=VP=11 <=> (x+1)(10-x) > 0 <=> -1 < 0 < 10

Chọn B
Cách giải: Ta có:
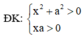
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
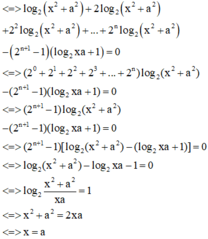
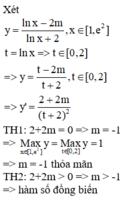
![]()

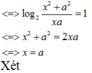
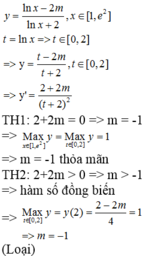
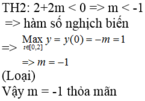
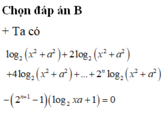









ta có |x+1|+|x-10|
=|x+1|+|10-x|
\(\ge\left|x+1+10-x\right|=\left|11\right|=\)\(11\)
Mà lại có |x+1|+|x-10|=11
=> Dấu = xảy ra khi (x+1)(10-x)\(\ge0\)
<=> \(-1\le x\le10\)
do x nguyên => s có 12 giá trị
tk mk nha bn