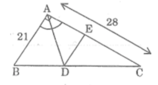
Bài 1.Tam giác ABC vuông tại A, có AB = 21cm, \(\widehat{C}\) = 40°, phân giác BD của góc ABC, D ∈ AC. Tính
a) độ dài đoạn thẳng AC, BC
b) độ dài đoạn thẳng BD
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính \(\widehat{B},\) \(\widehat{C}\)
Bài 3. Cho tam giác ABC vuông tại A có \(\widehat{B}\) = 30 °, AB = 6cm
a) Giải tam giác vuông ABC
b) Vẽ đường cao AH và trung tuyến Am của tam giác ABC. Tính diện tích tam giác AHM

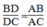 (t/chất đường phân giác)
(t/chất đường phân giác)
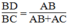
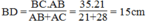
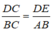 (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)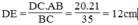
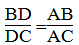 (t/chất đường phân giác)
(t/chất đường phân giác)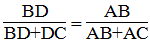
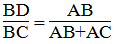
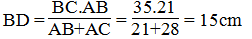
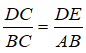 (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)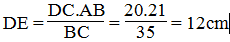

Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)